Củng cố kiến thức

1. Vectơ chỉ phương của lối thẳng

* Định nghĩa

Vectơ $\overrightarrow u $ được gọi là vectơ chỉ phương của đường thẳng liền mạch $\Delta $ nếu như $\overrightarrow u \ne \overrightarrow 0 $ và giá chỉ của $\overrightarrow u $ tuy vậy song hoặc trùng với $\Delta $.

Nhận xét

- Nếu $\overrightarrow u $ là 1 vectơ chỉ phương của lối thẳng $\Delta $ thì $k\overrightarrow u \left( {k \ne 0} \right)$ cũng là 1 vectơ chỉ phương của $\Delta $. Do bại một đường thẳng liền mạch đem vô số vectơ chỉ phương.

- Một đường thẳng liền mạch trọn vẹn được xác lập nếu như biết một điểm và một vectơ chỉ phương của đường thẳng liền mạch bại.

2. Phương trình thông số của lối thẳng

Định nghĩa

Trong mặt mày phẳng phiu Oxy cho tới lối thẳng $\Delta $đi qua điểm ${M_0}\left( {{x_0};{y_0}} \right)$ và nhận $\overrightarrow u = \left( {{u_1};{u_2}} \right)$ thực hiện vectơ chỉ phương. Với từng điểm M(x ; y) bất kì nhập mặt mày phẳng phiu, tao đem $\overrightarrow {M{M_0}} = \left( {x - {x_0};y - {y_0}} \right)$. Khi bại $M \in \Delta \Leftrightarrow \overrightarrow {M{M_0}} $ nằm trong phương với $\overrightarrow u \Leftrightarrow \overrightarrow {M{M_0}} = t\overrightarrow u $.

$ \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x - {x_0} = t{u_1}} \\
{y - {y_0} = t{u_2}}
\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{x = {x_0} + t{u_1}} \\
{y = {y_0} + t{u_2}}
\end{array}} \right.\left( 1 \right)$

Hệ phương trình (1) được gọi là phương trình thông số của lối thẳng $\Delta $, trong bại t là tham số.

Cho t một độ quý hiếm ví dụ thì tao xác lập được một điểm bên trên lối thẳng $\Delta $.

3. Vectơ pháp tuyến của đường thẳng liền mạch

Định nghĩa

Vectơ $\overrightarrow n $ được gọi là vectơ pháp tuyến của lối thẳng $\Delta $ nếu như $\overrightarrow n \ne 0$ và $\overrightarrow n $ vuông góc với vectơ chỉ phương của $\Delta $.

Nhận xét

Nếu $\overrightarrow n $ là 1 vectơ pháp tuyến của lối thẳng $\Delta $ thì $k\overrightarrow n \left( {k \ne 0} \right)$ cũng là một vectơ pháp tuyến của $\Delta $. Do bại một đường thẳng liền mạch đem vô số vectơ pháp tuyến.

Một đường thẳng liền mạch trọn vẹn được xác lập nếu biết một điểm và một vectơ pháp tuyến của chính nó.

4. Phương trình tổng quát lác của đưòng thẳng

Trong mặt mày phẳng phiu toạ chừng Oxy cho tới đường thẳng liền mạch $\Delta $ đi qua loa điểm ${M_0}\left( {{x_0};{y_0}} \right)$ và nhận $\overrightarrow n \left( {a;b} \right)$ thực hiện vectơ pháp tuyến.

Với từng điểm M(x ; y) bất kì nằm trong mặt mày phẳng phiu, tao có: $\overrightarrow {M{M_0}} = \left( {x - {x_0};y - {y_0}} \right)$.

Khi đó:

$\begin{array}{*{20}{l}}
{M\left( {x;y} \right) \in \Delta \Leftrightarrow \vec n \bot \overrightarrow {M{M_0}} } \\
{ \Leftrightarrow a\left( {x - {x_0}} \right) + b\left( {y - {y_0}} \right) = 0} \\
{ \Leftrightarrow ax + by + \left( { - a{x_0} - b{y_0}} \right) = 0} \\
{ \Leftrightarrow ax + by + c = 0}
\end{array}$

Với $c = - a{x_0} - b{y_0}$.

Định nghĩa

Phương trình ax + by + c =0 với a và b không đôi khi bởi vì 0, được gọi là phương trình tổng quát lác của đường thẳng liền mạch.

Nhận xét

Nếu lối thẳng $\Delta $có phương trình là ax + by + c = 0 thì $\Delta $có vectơ pháp tuyến là $\overrightarrow n = \left( {a;b} \right)$ và đem vectơ chỉ phương là $\overrightarrow u = \left( { - b;a} \right)$.

* Các tình huống quánh biệt

Cho đường thẳng liền mạch $\Delta $có phương trình tổng quát lác ax + by + c = 0 (1)

Xem thêm: học viện kỹ thuật quân sự điểm chuẩn

a) Nếu a = 0 phương trình (1) phát triển thành by + c = 0 hay $y = - \frac{c}{b}$.

Khi bại đường thẳng liền mạch $\Delta $vuông góc với trục Oy tại điểm $\left( {0; - \frac{c}{b}} \right)$.

b) Nếu b = 0 phương trình (1) phát triển thành ax + c = 0 hay $x = - \frac{c}{a}$.

Khi bại đường thẳng liền mạch $\Delta $vuông góc với trục Ox tại điểm $\left( { - \frac{c}{a};0} \right)$.

c) Nếu c = 0 phương trình (1) phát triển thành ax + by = 0.

Khi bại đường thẳng liền mạch $\Delta $đi qua loa gốc tọa chừng O.

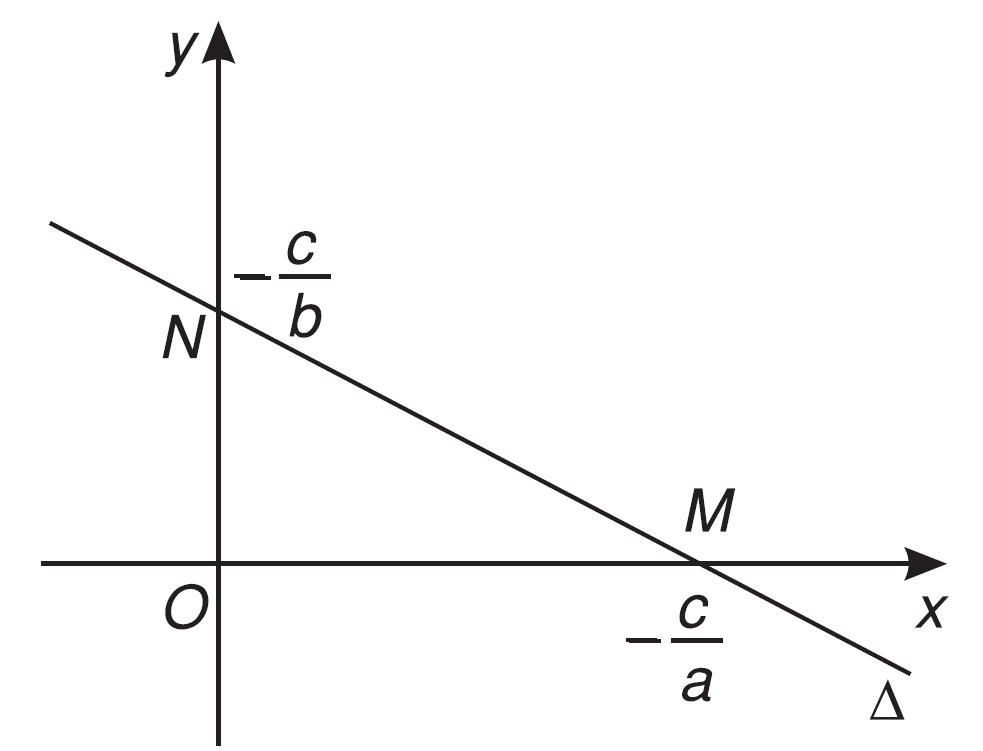
d) Nếu a, b, c đều không giống 0 tao rất có thể trả phương trình (1) về dạng $\frac{x}{{{a_0}}} + \frac{y}{{{b_0}}} = 1$.

với ${a_0} = - \frac{c}{a},{b_0} = - \frac{c}{b}$. (2). Phương trình này được gọi là phương trình đường thẳng liền mạch theo đuổi đoạn chắn, đường thẳng này hạn chế Ox và Oy lần lượt bên trên $M\left( {{a_0};0} \right)$ và $N\left( {0;{b_0}} \right)$.

5. Vị trí kha khá của hai tuyến đường thẳng

Xét hai tuyến đường trực tiếp ${\Delta _1}$ và ${\Delta _2}$ đem phương trình tổng quát lác thứu tự là ${a_1}x + {b_1}y + {c_1} = 0$ và ${a_2}x + {b_2}y + {c_2} = 0$.

Toạ chừng kí thác điểm của ${\Delta _1}$ và ${\Delta _2}$ là nghiệm của hệ phương trình:

$\left\{ {\begin{array}{*{20}{l}}
{{a_1}x + {b_1}y + {c_1} = 0} \\
{{a_2}x + {b_2}y + {c_2} = 0}
\end{array}} \right.(I)$

Ta đem những tình huống sau:

a) Hệ (I) mang trong mình một nghiệm $\left( {{x_0};{y_0}} \right)$, Lúc đó ${\Delta _1}$ cắt ${\Delta _2}$ tại điểm ${M_0}\left( {{x_0};{y_0}} \right)$.

b) Hệ (I) đem vô số nghiệm, Lúc bại ${\Delta _1}$ trùng với ${\Delta _2}$.

c) Hệ (I) vô nghiệm, Lúc đó ${\Delta _1}$ và ${\Delta _2}$ ko có điểm công cộng, hoặc ${\Delta _1}$ tuy vậy song với ${\Delta _2}$.

6. Góc thân thuộc hai tuyến đường trực tiếp

Góc thân thuộc hai tuyến đường trực tiếp ${\Delta _1}$ và ${\Delta _2}$ được kí hiệu là $\left( {\widehat {{\Delta _1},{\Delta _2}}} \right)$ hoặc $\left( {{\Delta _1},{\Delta _2}} \right)$.

Cho hai tuyến đường thẳng

$\begin{array}{*{20}{l}}
{{\Delta _1}:{a_1}x + {b_1}y + {c_1} = 0} \\
{{\Delta _2}:{a_2}x + {b_2}y + {c_2} = 0}
\end{array}$

Đặt $\varphi = \left( {\widehat {{\Delta _1},{\Delta _2}}} \right)$ thì tao thấy $\varphi $ bởi vì hoặc bù với góc giữa ${\overrightarrow n _{_1}}$ và ${\overrightarrow n _{_2}}$ nhập bại ${\overrightarrow n _{_1}}$, ${\overrightarrow n _{_2}}$ thứu tự là vectơ pháp tuyến của ${\Delta _1}$ và ${\Delta _2}$. Vì $\cos \varphi \ge 0$ nên ta suy ra

$\cos \varphi = \left| {\cos \left( {\overrightarrow {{n_1}} ,\overrightarrow {{n_2}} } \right)} \right| = \frac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|\left| {\overrightarrow {{n_2}} } \right|}}$

Vậy

$\cos \varphi = \frac{{\left| {{a_1}{a_2} + {b_1}{b_2}} \right|}}{{\sqrt {a_1^2 + b_1^2} \sqrt {a_2^2 + b_2^2} }}$.

Xem thêm: điểm chuẩn học viện báo chí và tuyên truyền 2022

7. Công thức tính khoảng cách từ là một điểm đến lựa chọn một lối thẳng

Trong mặt mày phẳng phiu Oxy cho tới lối thẳng $\Delta $có phương trình ax + by + c = 0 và điểm ${M_0}\left( {{x_0};{y_0}} \right)$. Khoảng cơ hội kể từ điểm ${M_0}$ cho tới đường thẳng liền mạch $\Delta $, kí hiệu là $d\left( {{M_0},\Delta } \right)$), được xem bởi công thức sau:

$d\left( {{M_0},\Delta } \right) = \frac{{\left| {a{x_0} + b{y_0} + c} \right|}}{{\sqrt {{a^2} + {b^2}} }}$