Giải Toán lớp 6 Kết nối trí thức, Cánh Diều, Chân trời sáng sủa tạo
Toán 6 bài bác 4 của 3 cuốn sách mới: Kết nối trí thức, Chân trời tạo nên, Cánh Diều với lời nói giải cụ thể, rõ rệt theo đòi khuông lịch trình sách giáo khoa Toán lớp 6. Lời giải hoặc bài bác luyện Toán 6 này bao gồm những bài bác giải ứng với từng bài học kinh nghiệm vô sách bám sát lịch trình học tập gom cho những em học viên ôn luyện và gia tăng những dạng bài bác luyện, tập luyện khả năng giải Toán.
Bạn đang xem: toán lớp 6 bài 4
1. Giải Toán lớp 6 bài bác 4 sách Kết nối trí thức với cuộc sống
Toán lớp 6 bài bác 4 Phép nằm trong và quy tắc trừ số ngẫu nhiên Kết nối trí thức sở hữu lời nói giải bám sát lịch trình học tập SGK. Toàn cỗ đáp án cụ thể mang lại từng phần, từng bài bác luyện vô nội dung lịch trình học tập Toán 6 sách mới nhất, gom những em học viên ôn luyện, gia tăng kỹ năng, rèn luyện Giải Toán 6 sách KNTT.
Toán lớp 6 luyện 1 trang 16 Câu 1.17
Tính:
a) 63 548 + 19 256
b) 129 107 + 34 693
Đáp án
a) 63 548 + 19 256 = 82 804
b) 129 107 + 34 693 = 163 800
Toán lớp 6 luyện 1 trang 16 Câu 1.18
Thay "?" ngay số quí hợp:
? + 2 895 = 2 895 + 6 789
Đáp án
Áp dụng đặc thù gửi gắm hoán của quy tắc nằm trong tao có:
? + 2 895 = 2 895 + 6 789. Suy đi ra "?" có mức giá trị 6 789
Toán lớp 6 luyện 1 trang 16 Câu 1.19
Tìm số ngẫu nhiên x thỏa mãn:
a) 7 + x = 362
b) 25 - x = 15
c) x - 56 = 4
Đáp án
a) 7 + x = 362
⇔ x = 362 - 7
⇔ x = 355
b) 25 - x = 15
⇔ x = 25 - 15
⇔ x = 10
c) x - 56 = 4
⇔ x = 56 + 4
⇔ x = 60
Toán lớp 6 luyện 1 trang 16 Câu 1.20
Dân số nước ta năm 2019 là 96 462 106 người. Năm 2020, số lượng dân sinh nước ta tăng 876 473 người đối với năm 2019. Tính số lượng dân sinh nước ta năm 2020. (Theo danso.org)
Đáp án
Dân số nước ta năm 2020 là:
96 462 106 + 876 473 = 97 338 579 (người)
Đáp số: 97 338 579 người
Toán lớp 6 luyện 1 trang 16 Câu 1.21
Nhà ga số 1 và căn nhà ga số 2 của một trường bay rất có thể tiêu thụ ứng khoảng tầm 6 526 300 và 3 514 500 lượt quý khách hàng năm. Nhờ đi vào dùng căn nhà ga số 3 tuy nhiên hàng năm trường bay này rất có thể tiếp sẽ có được khoảng tầm 22 851 200 lượt quý khách. Hãy tính số lượt quý khách tuy nhiên căn nhà ga số 3 rất có thể tiêu thụ hàng năm.
Đáp án
Tổng số lượt quý khách tuy nhiên căn nhà ga số 1 và số 2 rất có thể tiêu thụ hàng năm là:
6 526 300 + 3 514 500 = 10 040 800 (lượt)
Số lượt quý khách tuy nhiên căn nhà ga số 3 rất có thể tiêu thụ hàng năm là:
22 851 200 - 10 040 800 = 12 810 400 (lượt)
Đáp số: 12 810 400 lượt hành khách
Toán lớp 6 luyện 1 trang 16 Câu 1.22
Tính một cơ hội thích hợp lí:
a) 285 + 470 + 115 + 230
b) 571 + 216 + 129 + 124
Đáp án
a) 285 + 470 + 115 + 230
= (285 + 115) + (470 + 230)
= 400 + 700
= 1 100
b) 571 + 216 + 129 + 124
= (571 + 129) + (216 + 124)
= 700 + 340
= 1 040
Trắc nghiệm Toán 6 bài bác 4 KNTT
2. Giải Toán lớp 6 bài bác 4 sách Chân trời sáng sủa tạo
Toán lớp 6 bài bác 4 Lũy quá với số nón ngẫu nhiên CTST bao hàm đáp án cụ thể mang lại từng phần, từng bài bác luyện vô nội dung lịch trình học tập bài bác 4 Toán 6 trang 16, 17, 18 gom những em học viên ôn luyện, gia tăng kỹ năng, rèn luyện Giải Toán 6 sách Chân trời tạo nên.
Toán lớp 6 luyện 1 trang 18 Câu 1
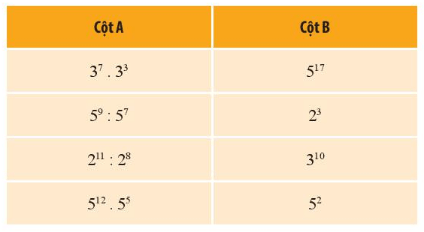
Ghép từng quy tắc tính ở cột A với lũy quá ứng của chính nó ở cột B.
Đáp án
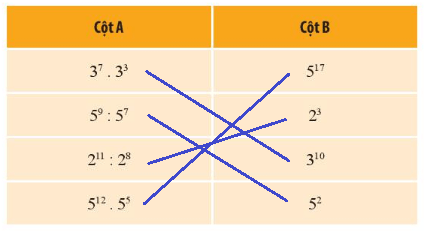
Toán lớp 6 luyện 1 trang 18 Câu 2
a) Viết thành phẩm của từng quy tắc tính sau bên dưới dạng một lũy thừa:
5 7 : 5 5 ; 9 5 : 8 0 ; 2 10 : 64 . 16.
b) Viết kết cấu thập phân của những số 4 983, 54 297, 2 023 theo đòi khuôn mẫu sau:
4 983 = 4 . 1000 + 9 . 100 + 8 . 10 + 3
= 4 . 10 3 + 9 . 10 2 + 8 . 10 + 3
Đáp án
a) 57 : 55 = 57 − 2 = 55 .
95 : 80 = 95 : 1 = 95 .
210 : 64 . 16 = 210 : 26 . 24 = 210 – 6 + 4 = 28 .
b) 54 297 = 5 . 10000 + 4 . 1000 + 2 . 100 + 9 . 10 + 7
= 5 . 10 3 = 4 . 103 + 2 . 102 + 9 . 10 + 7
2 023 = 2 . 1000 + 0. 100 + 2 . 10 + 3
= 2 . 103 + 2 . 10 + 3
Toán lớp 6 luyện 1 trang 18 Câu 3
Theo Tổng viên Thống kê, mon 10 năm 2020 số lượng dân sinh nước ta được sản xuất tròn trặn là 98 000 000 người. Em hãy ghi chép số lượng dân sinh của nước ta bên dưới dạng tích của một số trong những với cùng 1 lũy quá của 10.
Đáp án
Viết số lượng dân sinh của nước ta bên dưới dạng tích của một số trong những với cùng 1 lũy quá của 10 như sau:
98 000 000 = 98 . 106
Toán lớp 6 luyện 1 trang 18 Câu 4
Biết rằng lượng của Trái Đất khoảng tầm 6 00 … 000 (21 số 0) tấn, lượng của Mặt Trăng khoảng tầm 75 00 … 000 (18 số 0) tấn.
a) Em hãy ghi chép lượng của Trái Đất và lượng của Mặt Trăng bên dưới dạng tích của một số trong những với cùng 1 tích của một số trong những với cùng 1 lũy quá của 10.
b) Khối lượng Trái Đất vội vàng từng nào đợt lượng Mặt Trăng?
Đáp án
a) Khối lượng của Trái Đất = 6 . 1021 tấn
Khối lượng của Mặt Trăng = 75 . 1018 tấn
b) Khối lượng Trái Đất vội vàng lượng Mặt Trăng:
![]()
Trắc nghiệm Toán 6 bài bác 4 CTST
3. Giải Toán lớp 6 bài bác 4 sách Cánh Diều
Toán lớp 6 bài bác 4 Phép nhân, quy tắc phân chia những số ngẫu nhiên Cánh Diều bao hàm đáp án cụ thể mang lại từng phần, từng bài bác luyện vô nội dung lịch trình học tập bài bác 4 Toán 6, gom những em học viên ôn luyện, gia tăng kỹ năng, rèn luyện Giải Toán 6 sách Cánh Diều.
Toán lớp 6 trang 21 luyện 1 Bài 1
Tìm những số phù hợp ở lốt ?:
a) a . 0 = ?
b) a : 1 = ?
c) 0 : a = ? (với a ≠ 0 )
Đáp án
a) a. 0 = 0
b) a : 1 = a
c) 0 : a = 0
Toán lớp 6 trang 21 luyện 1 Bài 2
Tính một cơ hội thích hợp lí:
a) 50 . 347 . 2
b) 36 . 97 + 97 . 64
c) 157 . 289 - 289 . 57
Đáp án
a) 50 . 347 . 2 = (50 . 2) . 347 = 100 . 347 = 34 700
b) 36 . 97 + 97 . 64 = 97 . (36 + 64) = 97 . 100 = 9 700
c) 157 . 289 - 289 . 57 = 289 . (157 - 57) = 289 . 100 = 28 900
Toán lớp 6 trang 21 luyện 1 Bài 3
Đặt tính rồi tính:
a) 409 . 215
b) 54 322 : 346
c) 123 257 : 404
Đáp án
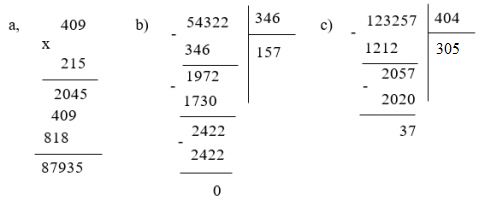
Toán lớp 6 trang 21 luyện 1 Bài 4
Một bênh nhân bị bức cao, thoát nước. Bác sĩ hướng dẫn và chỉ định húp 2 lít hỗn hợp Oresol nhằm bù nước. hiểu từng gói Oresol trộn với 200 ml nước. Bệnh nhân cơ nhớ dùng bao nhieu gói Oresol?
Đáp án
Đổi: 2 lít = 2000 ml
Bệnh nhân cơ nhớ dùng số gói Oresol là:
2000 : 200 = 10 (gói)
Toán lớp 6 trang 21 luyện 1 Bài 5
Một team thanh niên tự nguyện sở hữu 130 người cần thiết mướn xe hơi nhằm dịch chuyển. Họ cần thiết mướn tối thiểu từng nào nếu như từng xe pháo chở được 45 người?
Đáp án
Ta có:
130 : 45 = 2 dư 40
Vậy team thanh niên cần thiết mướn tối thiểu là 3 xe pháo xe hơi.
Toán lớp 6 trang 21 luyện 1 Bài 6
Lá cây chứa chấp thật nhiều hóa học diệp lục vô lục lạp thực hiện đặt lá cây làm nên màu xanh rớt. Tại lá thầu dầu, cứ 1 mm2 lá có tầm khoảng 500 000 lục lạp (Nguồn: Sinh học tập 6, NXB Giáo dục đào tạo nước ta, 2010).
Tính số lục lạp sở hữu bên trên một cái lá thầu dầu sở hữu diện tích S khoảng tầm 210 cm2
Đáp án
Ta có: 210 cm2 = 21000 mm2
Số lục lạp sở hữu bên trên một cái lá thầu dầu sở hữu diện tích S khoảng tầm 210 cm2 là:
Xem thêm: các loại so sánh trong tiếng anh
21000 . 500 000 = 10 500 000 000 (lục lạp)
Toán lớp 6 trang 21 luyện 1 Bài 7
Ở Bắc Sở, quy ước 1 thước = 24m2, 1 sào = 15 thước, 1 khuôn mẫu = 10 sào. Theo tay nghề nông gia, nhằm mạ đạt tiêu xài chuẩn chỉnh thì 1 sào ruộng cần thiết gieo khoảng tầm 2 kilogam thóc tương tự.
a) Để gieo mạ bên trên 1 khuôn mẫu ruộng cần thiết khoảng tầm từng nào ki-lô-gam thóc giống?
b) Để gửi gắm mạ bên trên 9 ha ruộng cần thiết khoảng tầm từng nào ki-lô-gam thóc giống?
Đáp án
a) 1 khuôn mẫu = 10 sào
Để gieo mạ bên trên 1 khuôn mẫu ruộng cần thiết khoảng tầm số ki-lô-gam thóc tương tự là:
10 . 2 = đôi mươi (kg)
b) 9 ha = 90 000 m2 = 3750 thước = 250 sào
Để gieo mạ bên trên 9 ha ruộng cần thiết khoảng tầm số ki-lô-gam thóc tương tự là:
250 . 2 = 500 (kg)
Toán lớp 6 trang 21 luyện 1 Bài 8
Sử dụng PC tóm tay:

Dùng PC di động nhằm tính:
275 x 356; 14 904 : 207; 15 x 47 x 216
Đáp án
Sử dụng PC di động tính tao được:
275 x 356 = 97 900
14 904 : 207 = 72
15 x 47 x 216 = 152 280
Trắc nghiệm Toán 6 bài bác 4 Cánh diều
Chuyên mục sách mới nhất Toán lớp 6 theo đòi lịch trình GDPT
- Toán lớp 6 Kết nối tri thức
- Toán lớp 6 Cánh Diều
- Toán lớp 6 Chân Trời Sáng Tạo
Tại trên đây bao gồm lời nói giải trọn vẹn cỗ của từng bài học kinh nghiệm của 3 sách mới nhất cả năm học tập. VnDoc liên tiếp update đáp án và lời nói giải mang lại chúng ta nằm trong theo đòi dõi.
4. Giải Toán lớp 6 bài bác 4 sách cũ
Tóm tắt lý thuyết Số thành phần của một tụ tập, Tập thích hợp con cái lớp 6
1. Một luyện hơp rất có thể sở hữu một thành phần, có rất nhiều thành phần, sở hữu vô số thành phần, cũng rất có thể không tồn tại thành phần nào là.
Tập thích hợp không tồn tại thành phần nào là được gọi là luyện trống rỗng và được kí hiệu là Φ.
2. Nếu một thành phần của tụ tập A đều nằm trong tụ tập B thì tụ tập A gọi là tụ tập con cái của tụ tập B.
Kí hiệu: A ⊂ B hoặc B ⊃ A và hiểu là:
A là tụ tập con cái của tụ tập B hoặc A được chứa chấp vô B hoặc B chứa chấp A.
Câu chất vấn 1 SGK Toán 6 trang 12
Các tụ tập sau sở hữu từng nào phần tử?
D = {0}, E = {bút, thước},
H={ x ∈ N| x≤10}
Phương pháp giải
Viết tụ tập H bằng phương pháp liệt kê những phần từ
Đếm số thành phần của những luyện hợp
Lời giải chi tiết
- Tập thích hợp D sở hữu một trong những phần tử là 0
- Tập thích hợp E sở hữu 2 thành phần là cây viết, thước
- Tập thích hợp H = { 0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10 } nên sở hữu 11 phần tử
Câu chất vấn 2 SGK Toán 6 trang 12
Tìm số ngẫu nhiên x tuy nhiên x+5=2
Phương pháp giải
Số hạng không biết bởi vì tổng trừ lên đường số hạng vẫn biết
Lời giải chi tiết
Ta sở hữu : x + 5=2
Suy đi ra x = 2 – 5
x = 2–5 (vô lý vì như thế 2 ko trừ được mang lại 5)
Vậy không tồn tại độ quý hiếm của x.
Câu chất vấn 3 SGK Toán 6 trang 12
Cho tía luyện hợp: M = {1; 5}, A = {1; 3; 5}, B = {5; 1; 3}.
Dùng kí hiệu ⊂ nhằm thể hiện tại mối quan hệ thân thiện nhì vô tía tình huống bên trên.
Phương pháp giải
Sử dụng tấp tểnh nghĩa: Nếu từng thành phần của tụ tập A đều nằm trong tụ tập B thì luyện A được gọi là luyện con cái của tụ tập B
Kí hiệu: A⊂B
Lời giải chi tiết
Ta có:
Tập thích hợp M sở hữu 2 thành phần là: 3; 5
Tập thích hợp A sở hữu 3 thành phần là: 1; 3; 5
Tập thích hợp B sở hữu 3 thành phần là: 5; 1; 3
Mọi thành phần của tụ tập M đều nằm trong tụ tập A nên M ⊂ A
Mọi thành phần của tụ tập M đều nằm trong tụ tập B nên M ⊂ B
Mọi thành phần của tụ tập A đều nằm trong tụ tập B nên A ⊂ B
Mọi thành phần của tụ tập B đều nằm trong tụ tập A nên B ⊂ A.
Giải Toán SGK Đại số 6 luyện 1 trang 13 Bài 16
Mỗi tụ tập sau sở hữu từng nào thành phần ?
a) Tập thích hợp A những số ngẫu nhiên x tuy nhiên x – 8 = 12
b) Tập thích hợp B những số ngẫu nhiên x tuy nhiên x + 7 = 7.
c) Tập thích hợp C những số ngẫu nhiên x tuy nhiên x. 0 = 0.
d) Tập thích hợp D những số ngẫu nhiên x tuy nhiên x. 0 = 3.
Hướng dẫn giải bài bác 1:
a) x – 8 = 12 Khi x = 12 + 8 = đôi mươi. Vậy A = {20}.
Nên tụ tập A sở hữu một trong những phần tử
b) x + 7 = 7 Khi x = 7 – 7 = 0. Vậy B = {0}.
Nên tụ tập B sở hữu một trong những phần tử
c) Với từng số ngẫu nhiên x tao đều phải sở hữu x. 0 = 0. Vậy C = N.
Nên tụ tập C sở hữu vô số thành phần.
d) Vì từng số ngẫu nhiên x tao đều phải sở hữu x. 0 = 0 nên không tồn tại số x nào là nhằm x. 0 = 3. Vậy D = Φ
Nên tụ tập D không tồn tại thành phần nào là.
Giải Toán SGK Đại số 6 luyện 1 trang 13 Bài 17
Viết những tụ tập sau và cho thấy từng tụ tập sở hữu từng nào phần tử?
a) Tập thích hợp A những số ngẫu nhiên ko vượt lên trước vượt đôi mươi.
b) Tập thích hợp B những số ngẫu nhiên to hơn 5 tuy nhiên nhỏ rộng lớn 6.
Phương pháp giải
Tìm tụ tập A, B bằng phương pháp liệt kê những thành phần tiếp sau đó điểm số thành phần của từng tụ tập.
Hướng dẫn giải bài bác 2:
a) Các số ngẫu nhiên ko vượt lên trước vượt đôi mươi là những số ngẫu nhiên nhỏ hơn hoặc bởi vì đôi mươi. Do cơ A = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16; 17; 18; 19; 20}. Như vậy A sở hữu 21 thành phần.
b) Giữa nhì số ngay lập tức nhau không tồn tại số ngẫu nhiên nào là nên B = Φ
Giải Toán SGK Đại số 6 luyện 1 trang 13 Bài 18
Cho A = {0}. cũng có thể bảo rằng A là tụ tập trống rỗng hoặc không?
Phương pháp giải
Tập trống rỗng là tụ tập không tồn tại một trong những phần tử nào
Bài giải:
Tập thích hợp A sở hữu một thành phần, này là số 0. Vậy A ko nên là tụ tập trống rỗng.
Giải Toán SGK Đại số 6 luyện 1 trang 13 Bài 19
Viết tụ tập A những số ngẫu nhiên nhỏ rộng lớn 10, tụ tập B những số ngẫu nhiên nhỏ rộng lớn 5, rồi người sử dụng kí hiệu ⊂ nhằm thể hiện tại mối quan hệ thân thiện nhì tụ tập bên trên.
Phương pháp giải
Nếu từng thành phần của tụ tập A đều nằm trong tụ tập B thì tụ tập A gọi là tụ tập con cái của tụ tập B.
Kí kiệu là: A ⊂ B
Lời giải chi tiết
A = {0; 1; 2; 3; 4; 5; 6; 7; 8; 9}; B = {0; 1; 2; 3; 4}. B ⊂ A
Giải Toán SGK Đại số 6 luyện 1 trang 13 Bài 20
Cho tụ tập A = {15; 24}. Điền kí hiệu ∈, ⊂ hoặc = vô dù rỗng mang lại đích.
a) 15 ...A;
b) {15}...A;
c) {15; 24}...A.
Phương pháp giải
+) Nếu a là một trong những phần tử của tụ tập A thì a ∈ A
+) Nếu từng thành phần của luyện A đều nằm trong tụ tập B thì A là luyện con cái của B. Kí hiệu: A⊂B.
+) Nếu A⊂B và B⊂A thì A=B
+) Cần phân biệt cơ hội ghi chép tụ tập và thành phần của tụ tập.
Chú ý: Nếu a là một trong những phần tử của tụ tập A thì cơ hội ghi chép {a} ∈ A là sai. Cách ghi chép thực sự {a} ⊂ A.
Lời giải chi tiết
a) 15 ∈ A.
b) {15} ko nên là một trong những thành phần tuy nhiên là một trong những tụ tập bao gồm duy nhất thành phần là số 15. Vì 15 ∈ A nên {15} ⊂ A.
Lưu ý. Nếu A là một trong những tụ tập và a ∈ A thì {a} ko nên là một trong những thành phần của tụ tập A tuy nhiên là một trong những tụ tập con cái bao gồm một thành phần của A.
Do cơ {a} ⊂ A. Vì vậy ghi chép {a} ∈ A là sai.
c) {15; 24} = A.
Xem thêm: tuổi trẻ và tương lai đất nước
Bài tiếp theo: Giải bài bác luyện Toán 6 trang 16 SGK luyện 1: Phép nằm trong và quy tắc nhân
Ngoài đi ra những em học viên rất có thể xem thêm những tư liệu tiếp thu kiến thức lớp 6 không giống bên trên VnDoc...và những đề đua học tập kì 1 lớp 6 và đề đua học tập kì 2 lớp 6 nhằm sẵn sàng cho những bài bác đua đề đua học tập kì đạt thành phẩm cao.
Tham khảo những dạng bài bác luyện môn Toán 6
- Giải bài bác luyện trang 6 SGK Toán lớp 6 luyện 1: Tập thích hợp, Phần tử của luyện hợp
- Giải bài bác luyện trang 7, 8 SGK Toán 6 luyện 1: Tập thích hợp những số tự động nhiên
- Giải bài bác luyện trang 10 SGK Toán lớp 6 luyện 1: Ghi số tự động nhiên













Bình luận