công thức tính s tam giác

Tính diện tích S tam giác đều là một trong những dạng toán thân thuộc và thông thường xuất hiện tại vô lịch trình toán học tập những cung cấp. Trong nội dung bài viết sau đây, Hoàng Hà Mobile tiếp tục chỉ dẫn các bạn phương pháp tính diện tích S tam giác đều và lối cao tam giác đều với những công thức chuẩn chỉnh nhất. Mời các bạn nằm trong tham lam khảo!

Trước lúc tới với phương pháp tính diện tích S tam giác đều, tất cả chúng ta tiếp tục nằm trong dò thám hiểu vài điều về định nghĩa, đặc thù và công thức tính diện tích S hình tam giác chung:

Bạn đang xem: công thức tính s tam giác

Hình tam giác là hình gì?

Trong hình học tập, hình tam giác là một trong những mô hình được tạo thành kể từ 3 cạnh và 3 đỉnh. Trong số đó, những điểm bên trên đỉnh ko nằm trong phía trên một đường thẳng liền mạch và tổng của 3 góc nằm trong lại luôn luôn trực tiếp bởi vì 180 chừng. 

Công thức công cộng dùng làm tính diện tích S hình tam giác

Để tính diện tích S hình tam giác, tất cả chúng ta cần thiết lấy tích của cạnh lòng với độ cao, tiếp sau đó phân chia cho tới 2. Công thức công cộng ví dụ tiếp tục là: 

S = ½ x (a x h)

Trong đó:

• a: chừng nhiều năm cạnh đáy
• h: độ cao nối kể từ đỉnh đối lập cạnh lòng và vuông góc với cạnh lòng tam giác

Lưu ý: Đây là công thức công cộng và các bạn được phép tắc vận dụng cho tới toàn bộ những hình tam giác không giống nhau, cho dù là phương pháp tính diện tích S tam giác đều cũng rất có thể dùng công thức này. 

Ví dụ: Cho hình tam giác ABC, sở hữu AH vuông góc với BC. lõi, AH = 6m, BC = 7m. Hãy tính diện tích S ABC?

Hướng dẫn giải:

Diện tích hình tam giác ABC là: (6 x 7) / 2 = 42 / 2 = 21 (m2). 

Vậy, diện tích S hình tam giác ABC là 21 mét vuông.

Nhận biết những loại tam giác vô hình học

Cần cảnh báo rằng, vô toán học tập sở hữu thật nhiều loại tam giác không giống nhau và chúng ta có thể phân biệt nhằm vận dụng phương pháp tính diện tích S tam giác đều, tam giác vuông… trải qua một số trong những điểm lưu ý tương quan cho tới góc, cạnh, ví dụ là:

• Tam giác thường: Tam giác này không tồn tại ngẫu nhiên điểm đặc biệt quan trọng này như không tồn tại góc vuông, không tồn tại cạnh hoặc góc này đều nhau. 
• Tam giác tù: Loại tam giác này tiếp tục chiếm hữu 1 góc to hơn 90 chừng. 
• Tam giác nhọn: Là tam giác được tạo thành kể từ 3 góc bé thêm hơn 90 chừng. 
• Tam giác vuông cân: Đây là tam giác chiếm hữu 1 góc vuông và 2 cạnh tạo thành góc vuông ấy có tính nhiều năm đều nhau. 
• Tam giác vuông: Tam giác vuông là hình tam giác chiếm hữu 1 góc bởi vì 90 chừng, được tạo thành bởi vì 2 cạnh góc vuông và cạnh còn sót lại là cạnh huyền.
• Tam giác cân: Đặc điểm nhận dạng của tam giác cân nặng là sở hữu 2 cạnh và 2 góc đều nhau. Trong số đó, 2 cạnh đều nhau là cạnh mặt mày, còn sót lại là cạnh lòng của hình tam giác.
• Tam giác đều: Đây là loại tam giác đặc biệt quan trọng, sở hữu 3 cạnh và 3 góc đều nhau (mỗi góc bởi vì 60 độ). Với những điểm lưu ý bên trên, chúng ta có thể dùng công thức và phương pháp tính diện tích S tam giác đều để sở hữu sản phẩm một cơ hội nhanh gọn lẹ rộng lớn. 

Tính hóa học của hình tam giác

Dưới đấy là những đặc thù cơ bạn dạng nhưng mà bạn phải nắm vững Khi ham muốn giải Việc sở hữu xuất hiện tại hình tam giác:

• Tính hóa học về góc: Tam giác luôn luôn sở hữu tổng của 3 góc bởi vì 180 chừng.
• Tính hóa học về cạnh: Khi nằm trong 2 cạnh ngẫu nhiên lại cùng nhau tiếp tục được một số lượng to hơn đối với cạnh còn sót lại. Chẳng hạn, tớ sở hữu a, b, c là 3 cạnh tam giác, vậy a + c > b, b + c > a và a + b > c. 
• 2 tam giác bởi vì nhau: Nếu 2 tam giác sở hữu những góc và cạnh ứng đều nhau, thì rất có thể suy đi ra 2 tam giác này đều nhau. 
• Tính hóa học lối cao: 1 tam giác sở hữu toàn bộ 3 lối cao. Trong số đó, lối cao được nối kể từ đỉnh cho tới cạnh đối lập và vuông góc với cạnh đối lập.
• Tính hóa học lối trung tuyến: 1 tam giác sở hữu toàn bộ 3 lối trung tuyến, được nối từ là 1 đỉnh cho tới trung điểm của cạnh đối lập. 

Cách tính diện tích S tam giác đều

Như vẫn nhắc phía trên, tam giác đều là một trong những dạng tam giác đặc biệt quan trọng. Khi hình tam giác sở hữu 1 trong số những điểm lưu ý sau, chúng ta có thể gọi cơ là một trong những tam giác đều:

• Tam giác sở hữu 3 cạnh đều nhau.
• Tam giác sở hữu 3 góc đều nhau và bởi vì 60 chừng.
• Tam giác cân nặng sở hữu 2 cạnh đều nhau và sở hữu 2 góc 60 chừng. 
• Tam giác sở hữu 2 góc bởi vì 60 chừng rất có thể được Tóm lại là tam giác đều.

Sau Khi Tóm lại được cơ là một trong những hình tam giác đều, chúng ta có thể tiến hành đo lường dựa vào đặc thù cơ bạn dạng sau:

• 3 góc đều nhau và bởi vì 60 chừng.
• Đường trung tuyến (cắt trung điểm của cạnh đáy) vô tam giác đều đôi khi cũng chính là lối phân giác (chia 1 góc trở thành 2 góc bởi vì nhau) và lối cao (vuông góc với cạnh đáy)

Khi cơ, tùy từng tài liệu đề bài bác cho tới nhưng mà chúng ta có thể vận dụng từng công thức không giống nhau như:

Trường phù hợp đề cho tới chiều nhiều năm 1 cạnh và chiều nhiều năm lối cao

Trong tình huống này, chúng ta có thể dùng công thức công cộng là: S = ½ x (a x h).

Ví dụ: 

Tính diện tích S tam giác đều ABC sở hữu lối cao là 12cm, chiều nhiều năm cạnh là 8cm:

=> Diện tích hình tam giác ABC là: (8 x 12) / 2 = 48 (cm2). 

Trường phù hợp đề chỉ cho tới chiều nhiều năm cạnh

Nếu như các bạn chỉ biết chiều nhiều năm của cạnh, chúng ta có thể nối 1 lối kể từ đỉnh cho tới lòng nhằm thực hiện lối cao. Lúc này, lối cao tiếp tục hạn chế cạnh đối lập bên trên trung điểm của cạnh cơ. Khi cơ, chúng ta có thể vận dụng công thức Pitago (a2 + b2 = c2) nhằm dò thám đi ra lối cao rồi vận dụng phương pháp tính diện tích S hình tam giác đều như tình huống bên trên. 

Hoặc, nhằm tiết kiệm chi phí thời hạn, các bạn cũng rất có thể người sử dụng trực tiếp công thức tính nhanh chóng sau:

S = (a^2 * √3) / 4

Tức là, tất cả chúng ta tiếp tục lấy bình phương chiều nhiều năm của cạnh tam giác đều nhân với √3 rồi phân chia cho tới 4 nhằm dò thám diện tích S hình tam giác đều. 

Ví dụ:

Cho một tam giác ABC sở hữu 3 cạnh đều nhau, từng cạnh nhiều năm 6cm, hãy tính diện tích S hình tam giác đó?

Tam giác ABC sở hữu 3 cạnh đều nhau nên rất có thể Tóm lại đấy là 1 tam giác đều, vận dụng công thức bên trên, tớ sở hữu diện tích S tam giác ABC bằng: 

S = (6^2 * √3) / 4 = 15.6 (cm2). 

Xem thêm: nhịp 2/4 là gì

Trường phù hợp đề đòi hỏi tính lối cao tam giác đều

Ngoài những phương pháp tính diện tích S tam giác đều bên trên, vô một số trong những tình huống, đề cũng rất có thể đòi hỏi các bạn tính độ cao tam giác đều. 

Trước lúc tới với chỉ dẫn cụ thể, bạn phải làm rõ đặc thù của lối cao vô tam giác đều: 

• Đường cao vô tam giác đều là lối được nối từ là 1 đỉnh cho tới trung điểm của cạnh lòng và vuông góc với cạnh lòng.
• Trong tam giác đều, 3 lối cao tiếp tục đều nhau và hạn chế nhau bên trên 1 điều – điểm đó là trọng tâm của hình tam giác. điều đặc biệt, Khi hạn chế nhau, bọn chúng tiếp tục vuông góc cùng nhau.
• Đối với tam giác đều, chúng ta có thể dò thám đi ra chiều nhiều năm được cao bởi vì công thức: h = a√3/2 (a là chiều nhiều năm cạnh vô tam giác). 

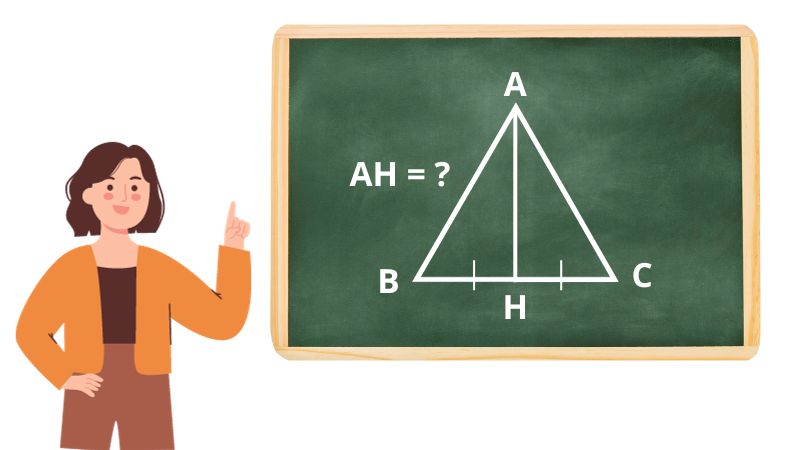
Ví dụ: Tính chiều nhiều năm lối cao AH của tam giác ABC, biết AB = 5cm?

Áp dụng công thức bên trên, tớ sở hữu AH = AB√3/2 = 5√3/2  = 4.33 (cm). 

Cách tính diện tích S những loại tam giác khác

Ngoài phương pháp tính diện tích S tam giác đều, các bạn cũng rất có thể vận dụng những công thức sau đây nhằm tính diện tích S của một số trong những loại tam giác thông thường bắt gặp khác:

Cách tính diện tích S tam giác cân

Với tam giác cân nặng, tớ sẽ có được 2 cạnh mặt mày đều nhau và lối cao nối kể từ đỉnh cho tới trung điểm của cạnh lòng. Công thức vẫn tương tự động là:

S = ½ x (a x h)

Trong cơ, a là chiều nhiều năm cạnh lòng, còn h là độ cao.

Ví dụ: Tính diện tích S hình tam giác cân nặng ABC với cạnh lòng bởi vì 10 centimet và lối cao bởi vì 7 cm?

Diện tích tam giác ABC là: S = (a x h) / 2 = (10 x 7) / 2 = 35 (cm2).

Cách tính diện tích S tam giác vuông

Vẫn với công thức S = ½ x (a x h), tuy nhiên trong tam giác vuông, a và h được hiểu là chiều nhiều năm của 2 cạnh góc vuông, 2 cạnh này vuông góc cùng nhau và nếu như lấy cạnh ngẫu nhiên thực hiện cạnh lòng thì cạnh còn sót lại sẽ tiến hành coi như lối cao. 

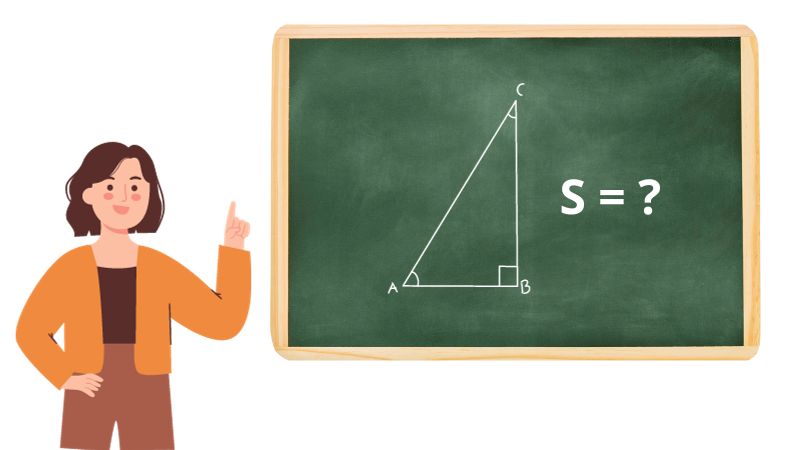
Ví dụ: Cho hình tam giác vuông ABC, vuông bên trên B, tính diện tích S ABC biết AB = 3m và BC = 4m.

Diện tích tam giác vuông ABC là: (3 x 4) / 2 = 6 (m2). 

Cách tính diện tích S tam giác vuông cân

Tương tự động với phương pháp tính diện tích S tam giác đều, tam giác vuông cân nặng cũng là một trong những hình tam giác đặc biệt quan trọng có một góc vuông được tạo thành kể từ 2 cạnh góc vuông đều nhau. Đồng thời, nhì góc còn sót lại cũng tiếp tục đều nhau, bởi vì 45 chừng.

Bạn rất có thể dùng công thức tính nhanh chóng sau:

S = a^2/2

Trong cơ, a là chừng nhiều năm cạnh lòng. 

Ví dụ: Cho tam giác ABC vuông bên trên A, sở hữu AB = AC = 5cm. Tìm diện tích S tam giác ABC?

Đầu tiên, tớ sở hữu ABC vuông bên trên B và 2 cạnh góc vuông đều nhau (đều bởi vì 5cm), nên rất có thể Tóm lại đấy là tam giác vuông cân nặng.

Khi cơ, chúng ta có thể dò thám cạnh lòng BC (tức là cạnh huyền tam giác) bởi vì công thức Pitago: AB^2 + AC^2 = BC^2 => BC = √50.

Vậy, diện tích S tam giác ABC = BC^2/2 = 50/2 = 25 (cm). 

Một số cảnh báo cần phải biết nhằm giải nhanh chóng những Việc tính diện tích S tam giác

Để giải chất lượng tốt những Việc tương quan cho tới diện tích S tam giác, bạn phải nắm vững một số trong những cảnh báo sau:

Hiểu rõ ràng đặc thù của từng loại tam giác

Việc làm rõ đặc thù giúp cho bạn đơn giản và dễ dàng phân biệt này là loại tam giác này, và nên vận dụng phương pháp tính diện tích S tam giác đều hoặc tam giác vuông… nhằm tiết kiệm chi phí thời hạn và sức lực lao động đo lường. Bên cạnh đó, đôi lúc đề sẽ không còn cho vừa toàn bộ tài liệu nhưng mà yên cầu người giải phải ghi nhận áp dụng trúng phương pháp để thể hiện sản phẩm đúng mực.

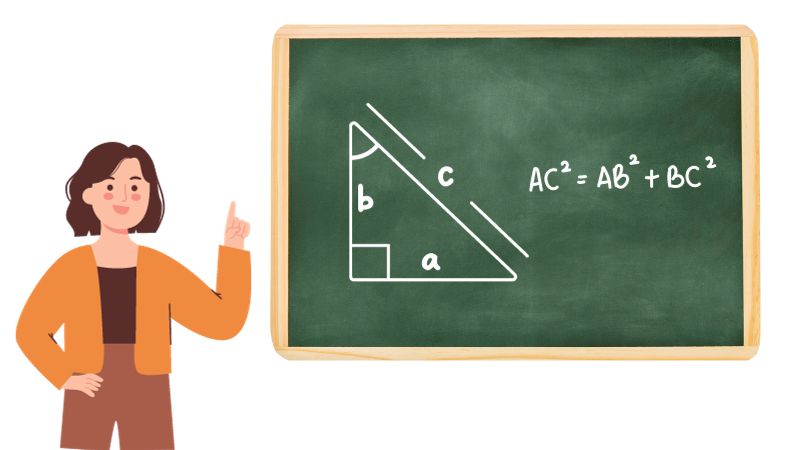
Kết phù hợp với quyết định lý Pitago

Khi giải những Việc tương quan cho tới tam giác vuông, các bạn thông thường nên kết phù hợp với công thức Pitago nhằm dò thám những dữ khiếu nại không đủ. Vậy nên, hãy đánh giá đề và tự động căn vặn liệu quyết định lý này còn có dùng được hay là không nhằm giải toán một cơ hội nhanh gọn lẹ, đơn giản và dễ dàng nhất nhé!

Thường xuyên luyện đề

Để nắm vững phương pháp tính diện tích S tam giác đều hoặc ngẫu nhiên loại tam giác này không giống, các bạn đều nên rèn luyện đề thông thường xuyên. Qua quy trình luyện đề, chúng ta có thể phân biệt được những dạng đề thông thường bắt gặp và rút đi ra cách thức giải thích hợp, hiệu suất cao nhất. Dù các bạn sở hữu xuất sắc toán hình hay là không, chỉ việc các bạn luôn luôn chịu khó, chắc hẳn rằng rằng các bạn sẽ giải được từng dạng toán mặc dù là nâng tối đa. 

Xem thêm: trắc nghiệm tâm lý học

Bên bên trên là phương pháp tính diện tích S tam giác đều và một số trong những loại tam giác không giống nhưng mà chúng ta có thể tìm hiểu thêm. Hy vọng nội dung bài viết tiếp tục hữu ích và hãy nhớ là share nhằm người xem nằm trong đón phát âm nhé!

Xem thêm:

• Tất cả điều các bạn cần phải biết về diện tích S mặt phẳng hình vỏ hộp chữ nhật
• Công thức phương pháp tính diện tích S và lối cao tam giác vuông