tính chất tứ giác nội tiếp

Tứ giác nội tiếp là tứ giác sở hữu tư đỉnh phía trên một đàng tròn trĩnh. Các đặc điểm của tứ giác nội tiếp bao gồm:
1. Tính hóa học 1: Tứ giác nội tiếp sở hữu tổng nhị góc đối vì chưng 180°. Vấn đề này tức là tổng của nhị góc kề vì chưng 180°.
2. Tính hóa học 2: Tứ giác nội tiếp sở hữu góc ngoài bên trên một đỉnh vì chưng góc nhập của đỉnh đối lập. Tức là góc ngoài bên trên một đỉnh của tứ giác nội tiếp vì chưng góc nhập bên trên đỉnh đối lập.
3. Tính hóa học 3: Tứ giác nội tiếp sở hữu 4 đỉnh cơ hội đều một điểm. Vấn đề này tức là những đỉnh của tứ giác đều phía trên một đàng tròn trĩnh và khoảng cách kể từ những đỉnh cho tới tâm đàng tròn trĩnh cũng đều bằng nhau.
4. Tính hóa học 4: Tứ giác nội tiếp sở hữu đàng trung tuyến là đàng kẻ kể từ tâm đàng tròn trĩnh cho tới trung điểm của nhị cạnh đối lập. Đường trung tuyến rời nhau bên trên một điểm độc nhất - đó là tâm đàng tròn trĩnh nội tiếp tứ giác.
5. Tính hóa học 5: Tứ giác nội tiếp sở hữu phân giác của một góc là 1 đường thẳng liền mạch trải qua tâm đàng tròn trĩnh. Tức là phân giác của một góc nhập tứ giác nội tiếp là 1 đoạn trực tiếp nối tâm đàng tròn trĩnh với phú điểm của nhị cạnh chứa chấp góc cơ.
6. Tính hóa học 6: Tứ giác nội tiếp sở hữu tứ diện nội tiếp. Vấn đề này tức là tổng tía góc nhập của tứ giác nội tiếp vì chưng 180°.
Nhờ nhập những đặc điểm này, tớ hoàn toàn có thể dễ dàng và đơn giản xác lập và đo lường những vấn đề tương quan cho tới tứ giác nội tiếp trong những câu hỏi hình học tập.

Bạn đang xem: tính chất tứ giác nội tiếp

Tứ giác nội tiếp là tứ giác sở hữu tư đỉnh phía trên và một đàng tròn trĩnh. Tính hóa học cần thiết của tứ giác nội tiếp bao gồm:
1. Tứ giác nội tiếp sở hữu tổng nhị góc đối vì chưng 180°: Vấn đề này tức là tổng nhị góc đối của tứ giác nội tiếp luôn luôn vì chưng 180°. Góc đối tiếp tạo ra vì chưng nhị cặp cạnh đối lập nhập tứ giác nội tiếp luôn luôn sở hữu tổng vì chưng 180°.
2. Tứ giác nội tiếp sở hữu góc ngoài bên trên một đỉnh vì chưng góc nhập của đỉnh đối diện: Vấn đề này tức là góc ngoài bên trên một đỉnh của tứ giác nội tiếp vì chưng góc nhập của đỉnh đối lập. Góc ngoài tạo ra vì chưng nhị cặp cạnh ko đỉnh chung với đỉnh ngoài nằm trong tứ giác nội tiếp.
3. Mọi tam giác đều phải sở hữu một đàng tròn trĩnh nước ngoài tiếp: Nghĩa là mặc dầu tam giác là tam giác thông thường, cân nặng, hoặc vuông, thì tam giác cơ đều phải sở hữu một đàng tròn trĩnh nước ngoài tiếp trải qua tía đỉnh của chính nó.
4. Tứ giác nội tiếp sở hữu tư đỉnh cơ hội đều một điểm trung tâm: Nếu vẽ hai tuyến đường chéo cánh của tứ giác nội tiếp, đàng chéo cánh này tiếp tục rời nhau bên trên một điểm và đàng này cũng chính là đàng trung trực của những đoạn trực tiếp nối những đỉnh với điểm trung tâm. Điểm rời chéo cánh và trung tâm của tứ giác nội tiếp được gọi là đỉnh ngày hè.

Tứ giác nội tiếp sở hữu tổng nhị góc đối vì chưng 180°.

Một tứ giác nội tiếp sở hữu 4 đỉnh. Tứ giác nội tiếp là 1 tứ giác sở hữu 4 đỉnh trực tiếp sản phẩm phía trên một đàng tròn trĩnh. Đáp án là 4 đỉnh.

Đúng, đặc điểm của tứ giác nội tiếp là tứ giác sở hữu góc ngoài bên trên một đỉnh vì chưng góc nhập của đỉnh đối lập. Để minh chứng đặc điểm này, tớ hoàn toàn có thể dùng những công thức tương quan cho tới góc của tứ giác nội tiếp.
1. Giả sử tứ giác ABCD là tứ giác nội tiếp, với AB là đàng chéo cánh.
2. Ta tiếp tục minh chứng rằng góc ngoài bên trên đỉnh A vì chưng góc nhập bên trên đỉnh C.
3. Theo ấn định lý góc nội tiếp, tứ giác ABCD sở hữu tổng nhị góc đối vì chưng 180°. Vì vậy, tớ sở hữu một vài góc sở hữu tổng vì chưng 180°.
4. Xét góc nội tiếp BAD và góc ngoài Ngân Hàng Á Châu ACB. Để đơn giản và giản dị, tớ gọi góc ngoài Ngân Hàng Á Châu ACB là x và góc nội tiếp BAD là nó.
5. Theo bước 3, tớ sở hữu góc ABD + góc BCD = 180°.
6. Vì tứ giác ABCD là tứ giác nội tiếp, tớ sở hữu góc ABD = góc DBC (góc đối).
7. Khi thay cho thế biểu thức góc ABD = góc DBC và góc ABD + góc BCD = 180° nhập biểu thức ở bước 5, tớ được nó + x = 180°.
8. Từ biểu thức này, tớ hoàn toàn có thể thấy rằng góc ngoài bên trên đỉnh A (x) vì chưng góc nhập bên trên đỉnh C (y), tức thị tính chất tứ giác nội tiếp sở hữu góc ngoài bên trên một đỉnh vì chưng góc nhập của đỉnh đối lập và được minh chứng.
Vậy, tớ hoàn toàn có thể tóm lại rằng đặc điểm của tứ giác nội tiếp là tứ giác sở hữu góc ngoài bên trên một đỉnh vì chưng góc nhập của đỉnh đối lập.

Có, tứ giác nội tiếp sở hữu một đàng tròn trĩnh nước ngoài tiếp. Vấn đề này hoàn toàn có thể được minh chứng vì chưng những đặc điểm sau đây:
- Tứ giác nội tiếp là tứ giác sở hữu tư đỉnh phía trên đàng tròn trĩnh cơ.
- Mỗi tam giác nhập tứ giác nội tiếp đều phải sở hữu một đàng tròn trĩnh nước ngoài tiếp. Vấn đề này tức là những đỉnh của tam giác cơ phía trên một đàng tròn trĩnh được gọi là đàng tròn trĩnh nước ngoài tiếp tam giác cơ.
- Do cơ, bằng phương pháp phối hợp những đàng tròn trĩnh nước ngoài tiếp của những tam giác nhập tứ giác nội tiếp, tớ hoàn toàn có thể kiến thiết được một đàng tròn trĩnh nước ngoài tiếp chứa chấp toàn bộ những đỉnh của tứ giác.
Vì vậy, tứ giác nội tiếp sở hữu một đàng tròn trĩnh nước ngoài tiếp.

Các đặc điểm của tứ giác nội tiếp như sau:
1. Tứ giác sở hữu tổng nhị góc đối vì chưng 180°: Tức là tổng nhị góc ở nhị đỉnh đối lập bên phía trong tứ giác nội tiếp luôn luôn vì chưng 180°.
2. Tứ giác sở hữu góc ngoài bên trên một đỉnh vì chưng góc nhập của đỉnh đối diện: Vấn đề này tức là góc ngoài bên trên một đỉnh của tứ giác nội tiếp luôn luôn vì chưng góc nhập của đỉnh đối lập phía trên nằm trong cung.
3. Tứ giác sở hữu 4 đỉnh cơ hội đều một điểm trung tâm: Tức là tứ giác nội tiếp sở hữu tâm là 1 điểm độc nhất và khoảng cách kể từ từng đỉnh cho tới tâm đều đều bằng nhau.
4. Mọi tam giác đều phải sở hữu một đàng tròn trĩnh nước ngoài tiếp: Tức là tam giác hoàn toàn có thể được nội tiếp vào trong 1 đàng tròn trĩnh độc nhất.
Riêng với tứ giác nội tiếp đàng tròn trĩnh, những đặc điểm không giống bao gồm:
5. Tứ giác nội tiếp đàng tròn trĩnh là tứ giác sở hữu tư đỉnh phía trên đàng tròn trĩnh cơ.
Các đặc điểm bên trên gom tất cả chúng ta nhận ra và phân loại những tứ giác nội tiếp trong những câu hỏi hình học tập.

Tứ giác nội tiếp là tứ giác sở hữu tư đỉnh phía trên một đàng tròn trĩnh. Vấn đề này tức là những đỉnh của tứ giác được điểm cơ hội đều một điểm phía trên đàng tròn trĩnh. Tức là cả tư góc của tứ giác đều nằm trong một đàng tròn trĩnh và sở hữu tâm cộng đồng là trung điểm của đàng tròn trĩnh cơ. Mọi tứ giác nội tiếp đều phải sở hữu một đàng tròn trĩnh nước ngoài tiếp.
Ngoài đi ra, sở hữu một vài đặc điểm không giống của tứ giác nội tiếp như:
- Tổng nhị góc đối của một tứ giác nội tiếp luôn luôn vì chưng 180°.
- Góc ngoài bên trên một đỉnh của tứ giác nội tiếp vì chưng góc nhập của đỉnh đối lập.
- Theo đặc điểm tam giác nội tiếp, tứ giác nội tiếp hoàn toàn có thể được xem như thể tứ giác xung quanh một tam giác nội tiếp, vì thế cả tư điểm đều phía trên đàng tròn trĩnh nước ngoài tiếp của tam giác.
Ví dụ: Trong một tứ giác nội tiếp ABCD, tớ hoàn toàn có thể tóm lại rằng góc BAC + góc BDC = 180°, góc ABD = góc BCD (theo tính chất tứ giác nội tiếp), và tứ giác ABDC xung quanh một tam giác nội tiếp.
Tóm lại, tứ giác nội tiếp là tứ giác sở hữu những đỉnh phía trên một đàng tròn trĩnh và sở hữu một vài đặc điểm quan trọng đặc biệt tương quan cho tới tổng những góc và mối quan hệ trong những góc của tứ giác.

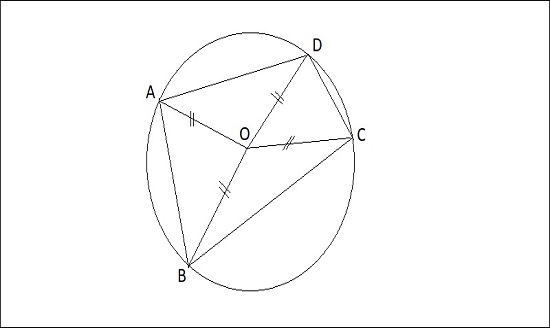
Một ví dụ rõ ràng về một tứ giác nội tiếp đàng tròn trĩnh hoàn toàn có thể là tứ giác ABCD phía trên đàng tròn trĩnh O.
Bước 1: Vẽ một đàng tròn trĩnh O ngẫu nhiên.
Bước 2: Chọn tư điểm A, B, C, D phía trên đàng tròn trĩnh O. Chúng tớ sở hữu tứ giác ABCD.
Bước 3: Kiểm tra coi những điểm A, B, C, D sở hữu phía trên đàng tròn trĩnh O hay là không bằng phương pháp đánh giá chừng nhiều năm 2 lần bán kính AB, BC, CD, DA. Nếu những đoạn trực tiếp này còn có nằm trong chừng nhiều năm và phân tách song 2 lần bán kính của đàng tròn trĩnh thì tứ giác ABCD là tứ giác nội tiếp đàng tròn trĩnh O.
Bước 4: Nếu tứ giác ABCD là tứ giác nội tiếp đàng tròn trĩnh O, tớ cũng hoàn toàn có thể xác lập được tâm đàng tròn trĩnh O. Tâm đàng tròn trĩnh O nằm ở vị trí tức thì trung điểm của hai tuyến đường chéo cánh AC và BD nhập tứ giác ABCD.
Vì vậy, ví dụ về một tứ giác nội tiếp đàng tròn trĩnh hoàn toàn có thể được xác lập bằng phương pháp lựa chọn tư điểm phía trên đàng tròn trĩnh và đánh giá coi những đoạn trực tiếp AB, BC, CD, DA sở hữu nằm trong chừng nhiều năm và phân tách song 2 lần bán kính của đàng tròn trĩnh hay là không.

Xem thêm: trường đại học công nghệ và quản lý hữu nghị

Đúng.
Tứ giác nội tiếp đàng tròn trĩnh là tứ giác sở hữu tư đỉnh phía trên đàng tròn trĩnh cơ. Tuy nhiên, tam giác ko thể là tứ giác nội tiếp vì thế nó chỉ mất tía đỉnh. Một tam giác hoàn toàn có thể sở hữu và một đàng tròn trĩnh nước ngoài tiếp với cùng một tứ giác nội tiếp không giống, tuy nhiên ko thể là tứ giác nội tiếp chủ yếu nó.