Đạo hàm sin2x là phần kỹ năng về đạo dung lượng giác thông thường bắt gặp nhập kỹ năng đạo hàm công tác Đại số Toán trung học tập phổ thông. Dạng bài xích tập dượt này xuất hiện nay không hề ít trong số đề đánh giá, bởi vậy sẽ giúp những em hiểu rằng những phương pháp tính đạo hàm sin2x đơn giản và giản dị, dễ dàng vận dụng, Marathon Education tiếp tục tổ hợp những lý thuyết này và share cho tới những em nhập nội dung bài viết sau đây.
>>> Xem thêm: Đạo Hàm Là Gì? Các Công Thức Tính Đạo Hàm Thường Gặp
Bạn đang xem: sin^2x đạo hàm
Đạo hàm của hắn = sinx
Để tính đạo hàm của hàm số hắn = sinx, tao tổ chức vận dụng công thức đạo dung lượng giác cơ phiên bản sau:
(sinx)’ = cosx
Cách tìm hiểu đạo hàm sin2x
Cách tính đạo hàm sin2x không vượt lên trên khó khăn. Cụ thể, những em rất có thể lựa chọn một trong các 2 cơ hội rõ ràng được nêu sau đây nhằm vận dụng giải những bài xích tập dượt tương quan cho tới phần kỹ năng này.
Tìm đạo hàm của hàm số hắn = sin2x
- Cách 1: kề dụng đạo dung lượng giác theo đòi hàm số u

Từ cơ, những em tiếp tục có:
(sin2x)’ = (2x)’.cos2x = 2.cos2x
- Cách 2: kề dụng đạo hàm một tích (u.v)’ = (u)’.v + (v)’.u
Từ cơ, những em tiếp tục có:
(sin2x)’ = 2(sinx.cosx)’
= 2[(sinx)’.cosx + sinx.(cosx)’]
= 2(cos2x – sin2x) = 2.cos2x.
Vậy đạo hàm của hàm số hắn = sin2x là 2cos2x
>>> Xem thêm: Cách Tìm Đạo Hàm Cos2x Và Bài Tập Vận Dụng Có Đáp Án
Cách tính đạo hàm của hàm số hắn = sin2x
Tính đạo hàm của hàm số hắn = sin2x
Xem thêm: kể chuyện đã nghe đã đọc
y’ = (sin2x)’ = 2sinx.(sinx)’ = 2sinx.cosx = sin2x
Vậy đạo hàm của hàm số hắn = sin2x là sin2x
>>> Xem thêm: Dạng Bài Tập Và Cách Giải Bất Phương Trình Toán Lớp 10
Đạo hàm của những hàm con số giác
Một số công thức đạo hàm cơ phiên bản của những hàm con số giác:
\begin{aligned}
&\bull \text{Hàm số hắn = sinx với đạo hàm }\forall x\in\R \text{ và }(sinx)'=cosx.\\
&\bull \text{Hàm số hắn = cosx với đạo hàm }\forall x\in\R \text{ và }(cosx)'=-sinx.\\
&\bull \text{Hàm số hắn = tanx với đạo hàm }\forall x\not=\frac{\pi}{2}+k\pi,\ k\in \R \text{ và }(tanx)'=\frac{1}{cos^2x}.\\
&\bull \text{Hàm số hắn = cotx với đạo hàm }\forall x\not=k\pi,\ k\in \R \text{ và }(cotx)'=-\frac{1}{sin^2x}.\\
\end{aligned}

Bảng tổ hợp đạo hàm của hàm con số giác cơ phiên bản và hàm con số giác ngược
Đạo hàm của hàm con số giác là phần kỹ năng cơ phiên bản. Dưới đấy là bảng đạo hàm cho những hàm con số giác cơ phiên bản và hàm con số giác ngược thông thường bắt gặp. Cụ thể như sau:
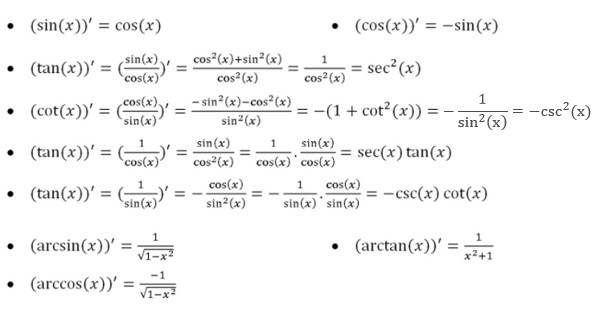
>>> Xem thêm: Tổng Hợp Các Kí Hiệu Trong Toán Học Phổ Biến Đầy Đủ Và Chi Tiết
Bài tập dượt áp dụng tính đạo hàm của sin2x
Quá trình học tập lý thuyết luôn luôn rất cần phải song song với thực hành thực tế. Có vì vậy, những em mới mẻ rất có thể dễ dàng và đơn giản hiểu bài xích và ghi ghi nhớ những công thức một cơ hội chất lượng rộng lớn. Để hùn những em “thuộc ở lòng” công thức tính đạo hàm sin2x, những em hãy nằm trong Marathon Education thực hành thực tế một trong những bài xích tập dượt áp dụng như sau đây.
Ví dụ 1: Tính đạo hàm của hàm số
Lời giải:
f'(x)=(sin2x-cos^23x)'=2cos2x+3sin3x.2cos3x=2cos2x+3sin6x
Ví dụ 2: Tính đạo hàm của hàm số:
y=\frac{sin2x+cos2x}{2sin2x-cos2x}
Lời giải:
Xem thêm: continue to v hay ving
\begin{aligned}
y'&=\left(\frac{sin2x+cos2x}{2sin2x-cos2x}\right)'\\
&=\frac{(sin2x+cos2x)'.(2sin2x-cos2x)-(2sin2x-cos2x)'.(sin2x+cos2x)}{(2sin2x-cos2x)^2}\\
&=\frac{(2cos2x – 2sin2x)(2sin2x – cos2x) – (4cos2x + 2sin2x)(sin2x + cos2x)}{(2sin2x-cos2x)^2}\\
&=\frac{–6cos^22x – 6sin^22x}{(2sin2x-cos2x)^2} = \frac{-6}{(2sin2x-cos2x)^2}
\end{aligned}
Tham khảo ngay lập tức những khoá học tập online của Marathon Education
Trên đấy là lý thuyết về đạo dung lượng giác giống như công thức và bài xích thói quen đạo hàm sin2x. Hy vọng sau khoản thời gian phát âm xong xuôi nội dung bài viết, những em rất có thể bắt được rất nhiều vấn đề hữu ích nhằm vận dụng nhập quy trình học hành của tớ.
Hãy tương tác ngay lập tức với Marathon sẽ được tư vấn nếu như những em mong muốn học trực tuyến nâng lên kỹ năng nhé! Marathon Education chúc những em được điểm trên cao trong số bài xích đánh giá và kỳ thi đua chuẩn bị tới!













Bình luận