Giới hạn hàm con số giác - Tất tần tật những vấn đề cần biết
Chủ đề Giới hạn hàm con số giác: Giới hạn hàm con số giác là 1 định nghĩa cần thiết nhập toán học tập, hùn tất cả chúng ta đo lường và nắm rõ rộng lớn về những hàm con số giác. bằng phẳng cơ hội dùng những công thức lượng giác, tao hoàn toàn có thể tính được số lượng giới hạn của hàm con số giác theo đòi lăm le lí 1. Vấn đề này hùn tất cả chúng ta thật nhiều trong những công việc nghiên cứu và phân tích và phần mềm của hàm con số giác trong số câu hỏi thực tiễn.
Bạn đang xem: lim sinx/x khi x tiến tới 0
Làm thế này nhằm tính số lượng giới hạn của một hàm con số giác?
Để tính số lượng giới hạn của một hàm con số giác, tất cả chúng ta dùng những công thức lượng giác cơ bạn dạng để lấy về dạng thích hợp. Sau bại liệt, vận dụng lăm le lí 1 của số lượng giới hạn nhằm đo lường. Dưới đấy là quy trình chi tiết:
Bước 1: Đưa hàm số về dạng thích hợp dùng công thức lượng giác:
- Kiểm tra coi nhập hàm số với tồn bên trên những lượng giác cơ bạn dạng như sin(x), cos(x), tan(x) ko. Nếu với, vận dụng những quy tắc quy đổi như sin(x) = 1/csc(x), cos(x) = 1/sec(x), tan(x) = 1/cot(x) để lấy về dạng thích hợp.
- Nếu với những biểu thức lũy quá, lấy những số nón thoát khỏi vết ngoặc cùng theo với hải dương thức và gửi về nhỏ dần dần của x (nếu có).
Bước 2: kề dụng lăm le lí 1 của giới hạn:
- Dựa nhập công thức lượng giác đã lấy về nhập bước 1, xác lập độ quý hiếm của những số lượng giới hạn riêng lẻ, bằng phương pháp thay cho x bởi độ quý hiếm tiến bộ cho tới nhập hàm.
Bước 3: Đánh giá chỉ giới hạn:
- Lấy những độ quý hiếm vẫn nhìn thấy nhập bước 2 và đo lường theo đòi công thức của số lượng giới hạn hàm số.
Bước 4: Kiểm tra độ quý hiếm giới hạn:
- Kiểm tra coi số lượng giới hạn chiếm được có mức giá trị xác lập hay là không bằng phương pháp coi liệu độ quý hiếm hàm số bên trên những điểm tiến bộ cho tới số lượng giới hạn với quy tụ hay là không.
- Nếu quy tụ và có mức giá trị xác lập, thì bại liệt đó là thành phẩm số lượng giới hạn của hàm con số giác.
Đây là quy trình tổng quát lác nhằm tính số lượng giới hạn của một hàm con số giác. Tuy nhiên, nhập tình huống rõ ràng và phức tạp rộng lớn, hoàn toàn có thể cần thiết vận dụng những công thức không giống và những quy tắc tương quan cho tới số lượng giới hạn hàm số.
Khái niệm \"giới hạn hàm con số giác\" nhắc đến quy trình xác lập số lượng giới hạn của những hàm con số giác, bao gồm những hàm số như sin(x), cos(x), tan(x), cot(x), sec(x) và csc(x), Khi x tiến bộ cho tới một độ quý hiếm rõ ràng.
Để tính số lượng giới hạn của một hàm con số giác, tất cả chúng ta cần thiết vận dụng những công thức và lăm le lý tương quan cho tới lượng giác. Một số công thức lượng giác cần thiết nhằm tính số lượng giới hạn là:
1. lim sin(x) = 0 Khi x tiến bộ cho tới 0
2. lim cos(x) = 1 Khi x tiến bộ cho tới 0
3. lim tan(x) = ∞ Khi x tiến bộ cho tới (2k + 1)π/2 (k là số nguyên)
4. lim cot(x) = ∞ Khi x tiến bộ cho tới kπ (k là số vẹn toàn ko phân chia không còn mang lại 2)
5. lim sec(x) = ko tồn bên trên (không nên là số hữu tỉ)
6. lim csc(x) = ko tồn bên trên (không nên là số hữu tỉ)
Còn nếu như hàm con số giác với biểu thức phức tạp rộng lớn, tất cả chúng ta cần thiết vận dụng những cách thức như quy đổi đổi mới, rút gọn gàng, phân tách hàm và vận dụng những lăm le lý nhằm xác lập số lượng giới hạn.
Với những công thức và lăm le lý tương quan cho tới lượng giác, tất cả chúng ta hoàn toàn có thể tính được số lượng giới hạn của những hàm con số giác Khi x tiến bộ cho tới một độ quý hiếm rõ ràng.
Định lí một trong tính số lượng giới hạn hàm con số giác tức là gì?
Định lí một trong tính số lượng giới hạn hàm con số giác là 1 quy tắc về số lượng giới hạn của những hàm con số giác. Định lí này tuyên bố rằng Khi x tiến bộ cho tới một độ quý hiếm thắt chặt và cố định (thường là 0) và những hàm số sin(x), cos(x), tan(x) với số lượng giới hạn xác lập, thì số lượng giới hạn của bọn chúng cũng rất được xác lập và được xem bằng phương pháp dùng số lượng giới hạn của bọn chúng được biết trước.
Cụ thể, theo đòi lăm le lí 1, Khi x tiến bộ cho tới 0, tao với những số lượng giới hạn sau:
- Giới hạn của hàm sin(x) Khi x tiến bộ cho tới 0 bởi 0.
- Giới hạn của hàm cos(x) Khi x tiến bộ cho tới 0 bởi 1.
- Giới hạn của hàm tan(x) Khi x tiến bộ cho tới 0 ko tồn bên trên hoặc ko xác lập.
Định lí 1 đỡ đần ta tính số lượng giới hạn của những hàm con số giác đơn giản dễ dàng rộng lớn bằng phương pháp dùng số lượng giới hạn của sin(x) và cos(x) được biết trước. Một số công thức lượng giác cũng rất được dùng nhằm đo lường những số lượng giới hạn này.
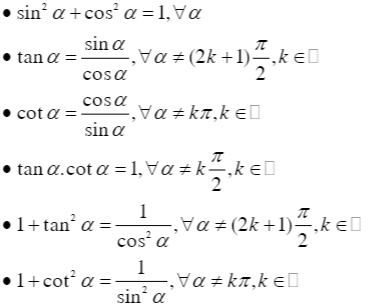
Giới hạn dạng 0/0 và số lượng giới hạn hàm con số giác - Môn toán lớp 11 - Thầy Nguyễn Công Chính
\"Giới hạn hàm con số giác - Cực hay! Giới hạn hàm con số giác\" là 1 video clip vô nằm trong mê hoặc và thú vị với những kỹ năng và kiến thức về hàm con số giác và số lượng giới hạn. Hãy thám thính hiểu phương pháp tính số lượng giới hạn và vận dụng nhập bài xích tập dượt cực kỳ hoặc ngay lập tức bây giờ!
Các công thức lượng giác cần thiết nắm rõ nhằm tính số lượng giới hạn hàm con số giác là gì?
Các công thức lượng giác cần thiết nắm rõ nhằm tính số lượng giới hạn hàm con số giác bao gồm:
1. Giá trị của sin(x) và cos(x):
- sin(0) = 0
- cos(0) = 1
- sin(π/6) = 1/2
- cos(π/6) = √3/2
- sin(π/4) = √2/2
- cos(π/4) = √2/2
- sin(π/3) = √3/2
- cos(π/3) = 1/2
2. Các công thức chuyển đổi nhập lượng giác:
- sin(-x) = -sin(x)
- cos(-x) = cos(x)
- sin(x±y) = sin(x)cos(y) ± cos(x)sin(y)
- cos(x±y) = cos(x)cos(y) ∓ sin(x)sin(y)
3. Công thức contact thân ái tan(x) và sin(x), cos(x):
- tan(x) = sin(x)/cos(x)
4. Các số lượng giới hạn cơ bạn dạng của hàm con số giác:
- Giới hạn của sin(x) Khi x tiến bộ cho tới 0 là 1 trong những.
- Giới hạn của cos(x) Khi x tiến bộ cho tới 0 là 1 trong những.
- Giới hạn của tan(x) Khi x tiến bộ cho tới 0 là 0.
- Giới hạn của sin(x)/x Khi x tiến bộ cho tới 0 là 1 trong những.
- Giới hạn của (1-cos(x))/x Khi x tiến bộ cho tới 0 là 0.
- Giới hạn của (1-cos(x))/x^2 Khi x tiến bộ cho tới 0 là một nửa.
Nắm vững vàng những công thức và số lượng giới hạn bên trên sẽ hỗ trợ đo lường số lượng giới hạn của những hàm con số giác một cơ hội đúng chuẩn và hiệu suất cao.
Làm thế này nhằm tính số lượng giới hạn của hàm con số giác theo đòi lăm le lí 1?
Để tính số lượng giới hạn của hàm con số giác theo đòi lăm le lý 1, tao hoàn toàn có thể thực hiện như sau:
Bước 1: Xác định vị trị x sát cho tới số lượng giới hạn của hàm số.
Bước 2: Sử dụng lăm le lý 1 nhằm tính số lượng giới hạn của hàm số.
Định lý 1: Khi x tiến bộ sát cho tới một độ quý hiếm thắt chặt và cố định a, hàm con số giác sin(x) và cos(x) cũng tiến bộ sát cho tới một độ quý hiếm thắt chặt và cố định theo thứ tự là sin(a) và cos(a).
Ví dụ: Tính số lượng giới hạn của hàm số f(x) = sin(x) Khi x tiến bộ sát cho tới 0.
Bước 1: Xác định vị trị x sát cho tới số lượng giới hạn của hàm số. Tại phía trên, độ quý hiếm 0 sát cho tới số lượng giới hạn của hàm số.
Bước 2: kề dụng lăm le lý 1, Khi x tiến bộ sát cho tới 0, hàm con số giác sin(x) cũng tiến bộ sát cho tới sin(0) = 0. Vì vậy, số lượng giới hạn của hàm số f(x) = sin(x) Khi x tiến bộ sát cho tới 0 là 0.
Với từng câu hỏi rõ ràng, tất cả chúng ta cần thiết thay cho thay đổi độ quý hiếm của x và xác lập độ quý hiếm số lượng giới hạn của hàm con số giác ứng.
_HOOK_
Xem thêm: trang trí hội trường lớp 9
Giới hạn hàm con số giác - Cực hay!
\"Tìm Giới hạn của hàm con số giác Giới hạn hàm con số giác\" là video clip tuyệt đối hoàn hảo mang lại những chúng ta đang được học tập toán lớp
Đặc điểm và công việc quy tắc Khi tính số lượng giới hạn hàm con số giác?
Đặc điểm của số lượng giới hạn hàm con số giác là nhập quy trình đo lường, tất cả chúng ta dùng những công thức lượng giác nhằm xác lập độ quý hiếm số lượng giới hạn của hàm số. Có một vài bước quy tắc cơ bạn dạng Khi tính số lượng giới hạn hàm con số giác như sau:
1. Xác lăm le coi số lượng giới hạn với dạng sin(x), cos(x) hoặc tan(x), hay như là 1 sự phối kết hợp của bọn chúng. Vấn đề này cực kỳ cần thiết nhằm hoàn toàn có thể vận dụng những công thức lượng giác thích hợp.
2. Sử dụng những quy tắc số lượng giới hạn cơ bạn dạng, như quy tắc số lượng giới hạn của tổng, hiệu, tích và thương, để lấy số lượng giới hạn hàm số về dạng tuy nhiên tất cả chúng ta hoàn toàn có thể vận dụng những công thức lượng giác.
3. Xác định vị trị của những lượng giác cơ bạn dạng như sin(x), cos(x) và tan(x) bên trên những độ quý hiếm sát số lượng giới hạn. Sử dụng báo giá trị hoặc PC nhằm đo lường những độ quý hiếm này.
4. kề dụng những quy tắc số lượng giới hạn lượng giác rõ ràng nhằm tính độ quý hiếm số lượng giới hạn của hàm con số giác. Các quy tắc này bao hàm những công thức lượng giác cơ bạn dạng như sin(a + b), sin(a - b), cos(a + b), cos(a - b), tan(a + b), tan(a - b), và những công thức chuyển đổi không giống.
5. Từ thành phẩm đo lường được, tao hoàn toàn có thể suy đi ra số lượng giới hạn của hàm con số giác bên trên điểm xác lập.
Nhớ đánh giá kỹ những công thức lượng giác tuy nhiên chúng ta dùng nhằm đáp ứng đo lường đúng chuẩn. Nếu quan trọng, dùng PC hoặc phần mềm địa hình nhằm đo lường một vài độ quý hiếm khó tính khó nết.
Hy vọng rằng câu vấn đáp này giúp cho bạn hiểu phương pháp tính số lượng giới hạn hàm con số giác một cơ hội cụ thể.
Làm thế này nhằm thám thính số lượng giới hạn của những biểu thức chứa chấp hàm con số giác?
Để thám thính số lượng giới hạn của những biểu thức chứa chấp hàm con số giác, tao tiến hành công việc sau:
Bước 1: Phân tích biểu thức chứa chấp hàm con số giác và xác lập những số lượng giới hạn riêng biệt của những hàm con số giác nhập biểu thức.
Bước 2: Xác định vị trị tầm của biểu thức Khi tiến bộ cho tới số lượng giới hạn. Đối với những biểu thức chứa chấp hàm con số giác, tao hay sử dụng những công thức lượng giác cơ bạn dạng nhằm đo lường.
Bước 3: Sử dụng quy tắc nhân và phân chia nhằm đo lường biểu thức và thám thính độ quý hiếm tầm của biểu thức Khi tiến bộ cho tới số lượng giới hạn.
Bước 4: Xác lăm le số lượng giới hạn sau cùng của biểu thức bằng phương pháp dùng công thức số lượng giới hạn của những hàm con số giác.
Lưu ý: Việc thám thính số lượng giới hạn của biểu thức chứa chấp hàm con số giác hoàn toàn có thể phức tạp và yên cầu sự đúng chuẩn nhập đo lường. Do bại liệt, cần thiết tiến hành công việc đo lường cảnh giác và dùng công thức đúng chuẩn nhằm đáp ứng thành phẩm đúng chuẩn.

Các ví dụ minh họa và bài xích tập dượt tương quan cho tới tính số lượng giới hạn của hàm con số giác?
Để tính số lượng giới hạn của hàm con số giác, tất cả chúng ta hoàn toàn có thể dùng những công thức lượng giác cơ bạn dạng và lăm le lí số lượng giới hạn của hàm. Dưới đấy là một vài ví dụ minh họa và bài xích tập dượt tương quan cho tới tính số lượng giới hạn của hàm con số giác:
Ví dụ 1: Tính số lượng giới hạn của hàm con số giác sin(x) Khi x tiến bộ cho tới 0.
Giải:
Ta hoàn toàn có thể dùng lăm le lí số lượng giới hạn của hàm nhằm giải câu hỏi này.
Với hàm số sin(x), Khi x tiến bộ cho tới 0, tao hoàn toàn có thể thấy rằng độ quý hiếm của hàm cũng tiến bộ cho tới 0.
Do bại liệt, số lượng giới hạn của hàm con số giác sin(x) Khi x tiến bộ cho tới 0 là 0.
Ví dụ 2: Tính số lượng giới hạn của hàm con số giác cos(x) Khi x tiến bộ cho tới pi/2.
Giải:
Ta cũng hoàn toàn có thể dùng lăm le lí số lượng giới hạn của hàm nhập tình huống này.
Khi x tiến bộ cho tới pi/2, độ quý hiếm của cos(x) tiến bộ cho tới 0.
Vì vậy, số lượng giới hạn của hàm con số giác cos(x) Khi x tiến bộ cho tới pi/2 là 0.
Ví dụ 3: Tính số lượng giới hạn của hàm con số giác tan(x) Khi x tiến bộ cho tới pi/4.
Giải:
Đối với hàm số tan(x), Khi x tiến bộ cho tới pi/4, độ quý hiếm của hàm sẽ không còn tồn bên trên vì như thế tử số là số thực không giống 0 và khuôn số tiến bộ cho tới 0.
Vì vậy, không tồn tại số lượng giới hạn của hàm con số giác tan(x) Khi x tiến bộ cho tới pi/4.
Trên đấy là một vài ví dụ minh họa và bài xích tập dượt tương quan cho tới tính số lượng giới hạn của hàm con số giác. Các bài xích tập dượt này đòi hỏi tao dùng kỹ năng và kiến thức về công thức lượng giác và lăm le lí số lượng giới hạn của hàm nhằm xử lý.
Toán 11 - Tìm Giới hạn của hàm con số giác
Hãy coi video clip nhằm thám thính hiểu cơ hội thám thính số lượng giới hạn của hàm con số giác một cơ hội đơn giản dễ dàng và cụ thể nhất. Nắm vững vàng kỹ năng và kiến thức và nâng du lịch số của bạn!
Tính hóa học và quy tắc vận dụng Khi tính số lượng giới hạn của hàm con số giác trong số câu hỏi phức tạp?
Để tính số lượng giới hạn của hàm con số giác trong số câu hỏi phức tạp, tất cả chúng ta hoàn toàn có thể vận dụng những quy tắc và đặc thù như sau:
1. Sử dụng những quy tắc cơ bạn dạng nhập số lượng giới hạn hàm con số giác:
- Quy tắc cộng: Giới hạn của tổng nhị hàm số là tổng của số lượng giới hạn của từng hàm số.
- Quy tắc nhân với cùng một số: Giới hạn của một hàm số Khi nhân với một vài là số lượng giới hạn của hàm số nhân với độ quý hiếm bại liệt.
- Quy tắc chia: Giới hạn của một hàm số Khi phân chia cho 1 hàm số không giống là số lượng giới hạn của thương của nhị hàm số (với ĐK hàm số phân chia không giống ko ở điểm giới hạn).
2. Sử dụng những công thức lượng giác cơ bản:
- Công thức sin(a + b) = sin(a)cos(b) + cos(a)sin(b)
- Công thức cos(a + b) = cos(a)cos(b) - sin(a)sin(b)
- Công thức tan(a + b) = (tan(a) + tan(b))/(1 - tan(a)tan(b))
3. Chia nhỏ biểu thức: Trong tình huống những biểu thức phức tạp, tất cả chúng ta hoàn toàn có thể phân chia nhỏ hàm số trở thành những bộ phận nhỏ rộng lớn nhằm đơn giản dễ dàng tính số lượng giới hạn.
4. Sử dụng công thức giới hạn: Có một vài công thức số lượng giới hạn đang được minh chứng nhằm tính những số lượng giới hạn của hàm con số giác:
- Giới hạn sin(x)/x Khi x tiến bộ cho tới 0 là 1 trong những.
- Giới hạn tan(x)/x Khi x tiến bộ cho tới 0 là 1 trong những.
- Giới hạn (1 - cos(x))/x Khi x tiến bộ cho tới 0 là 0.
5. Định lí giới hạn:
- Định lí 1: Giới hạn của hàm sin(x) Khi x tiến bộ cho tới 0 là 1 trong những.
- Định lí 2: Giới hạn của hàm cos(x) Khi x tiến bộ cho tới 0 là 0.
Sử dụng những quy tắc, công thức và lăm le lí bên trên, tất cả chúng ta hoàn toàn có thể đo lường số lượng giới hạn của hàm con số giác trong số câu hỏi phức tạp.
Xem thêm: 5 lần đổi tên của đảng cộng sản việt nam

Ứng dụng thực tiễn của số lượng giới hạn hàm con số giác trong số nghành như vật lý cơ, nghệ thuật, và toán học tập ứng dụng?
Giới hạn hàm con số giác là 1 định nghĩa cần thiết được dùng trong tương đối nhiều nghành không giống nhau như vật lý cơ, nghệ thuật và toán học tập phần mềm. Dưới đấy là những phần mềm rõ ràng của số lượng giới hạn hàm con số giác trong số nghành này:
1. Vật lý: Trong vật lý cơ, số lượng giới hạn hàm con số giác được vận dụng nhằm tế bào miêu tả và đưa ra quyết định về những hiện tượng lạ giao động và đổi mới thiên trong số khối hệ thống dựa vào cấu hình sóng. Ví dụ, nhập năng lượng điện kể từ học tập, số lượng giới hạn của hàm số cực kỳ trị được dùng nhằm đo lường về sóng năng lượng điện kể từ và xác định rõ địa điểm của những điểm nút và đỉnh sóng.
2. Kỹ thuật: Trong nghệ thuật, số lượng giới hạn hàm con số giác được dùng nhằm phân tách và kiến thiết những khối hệ thống giao động và đổi mới thiên. Chẳng hạn, nhập nghệ thuật năng lượng điện tử, số lượng giới hạn hàm con số giác được vận dụng nhằm đo lường tần số hạn chế và dải tần số của những mạch thanh lọc, đáp ứng sự ổn định lăm le và unique tín hiệu.
3. Toán học tập ứng dụng: Trong toán học tập, số lượng giới hạn hàm con số giác được dùng trong số luật lệ tính chuẩn chỉnh xác và giải những câu hỏi phức tạp. Chẳng hạn, nhập phân tách và vi tích phân, số lượng giới hạn hàm con số giác được dùng nhằm đo lường đạo hàm và tích phân của những hàm con số giác, kể từ bại liệt thám thính đi ra độ quý hiếm tối ưu và đàng cong của những đồ gia dụng thị hàm số.
Các phần mềm của số lượng giới hạn hàm con số giác không chỉ là số lượng giới hạn nhập vật lý cơ, nghệ thuật và toán học tập, mà còn phải được vận dụng rộng thoải mái trong tương đối nhiều nghành khác ví như tài chính, chất hóa học, sinh học tập và tổng hợp. Hiểu và vận dụng số lượng giới hạn hàm con số giác đúng cách dán cực kỳ cần thiết nhằm hiểu và xử lý những yếu tố phức tạp trong số nghành này.
_HOOK_












Bình luận