trực tâm của tam giác

Trực tâm của tam giác là vấn đề phó của tía lối cao. Đường cao nhập tam giác là đoạn trực tiếp nối một đỉnh của tam giác với đối lập của chính nó và trải qua trực tâm. Cụ thể, tao hoàn toàn có thể xác lập trực tâm bằng phương pháp lần phó điểm của những lối cao nhập tam giác. Mỗi tam giác sở hữu chính một trực tâm và điểm đó trực thuộc tam giác.

Bạn đang xem: trực tâm của tam giác

Trực tâm của tam giác là vấn đề trùng với phó điểm của tía lối cao nhập tam giác bại liệt. Đường cao nhập tam giác là đoạn trực tiếp liên kết một đỉnh của tam giác với điểm trung điểm (tâm) của cạnh đối lập.
Cách lần trực tâm của tam giác được triển khai như sau:
1. Vẽ tam giác và đánh giá những đỉnh là A, B và C.
2. Vẽ lối cao kể từ từng đỉnh. Đường cao này là đoạn liên kết đỉnh với điểm trung điểm của cạnh đối lập. Việc vẽ lối cao này hoàn toàn có thể triển khai bằng phương pháp dùng thước kẻ và viên cây bút khắc ghi.
3. Tìm phó điểm của tía lối cao. Điểm này đó là trực tâm của tam giác.
Trực tâm của tam giác là 1 trong những điểm cần thiết nhập tam giác cũng chính vì nó là vấn đề phó của tía lối cao. Đặc điểm cần thiết của trực tâm là nó nằm cạnh nhập tam giác, ko phía trên cạnh hoặc ngoài tam giác.

Một tam giác sở hữu chính một trực tâm. Trực tâm của tam giác là vấn đề phó của tía lối cao của tam giác bại liệt. Đường cao nhập tam giác là đoạn trực tiếp vuông góc liên kết một đỉnh của tam giác cho tới cạnh đối lập.

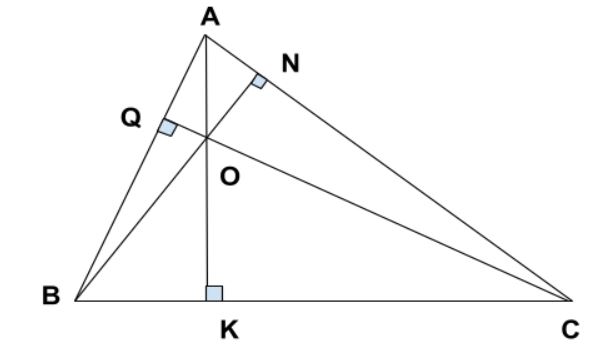
Trực tâm của tam giác nằm tại nút giao của tía lối cao nhập tam giác bại liệt. Đường cao nhập tam giác là đoạn trực tiếp liên kết một đỉnh của tam giác cho tới một cạnh đối lập sao cho tới tạo ra trở thành một góc vuông.
Để xác lập trực tâm của tam giác, tao hoàn toàn có thể tuân theo công việc sau:
Bước 1: Vẽ tam giác ngẫu nhiên.
Bước 2: Vẽ những lối cao kể từ từng đỉnh của tam giác. Để vẽ được lối cao, tao nên biết được phỏng lâu năm những cạnh của tam giác.
Bước 3: Tìm nút giao của tía lối cao kể từ bước 2. Điểm này được gọi là trực tâm của tam giác.
Ví dụ, nhằm lần trực tâm của tam giác ABC, tao triển khai công việc sau:
Bước 1: Vẽ tam giác ABC.
Bước 2: Vẽ những lối cao AH, BK và CL kể từ từng đỉnh của tam giác.
Bước 3: Tìm nút giao của tía lối cao AH, BK và CL. Điểm này đó là trực tâm của tam giác ABC.
Lưu ý rằng trực tâm của tam giác ko nhất thiết phía trên cạnh tam giác, nó hoàn toàn có thể trực thuộc tam giác hoặc ngoài tam giác tùy nhập hình dạng của tam giác bại liệt.

Để tính được trực tâm của tam giác, tao nên biết rằng trực tâm là vấn đề phó của tía lối cao. Đường cao nhập tam giác là đoạn trực tiếp liên kết một đỉnh của tam giác với đối lập của chính nó và vuông góc với đường thẳng liền mạch bại liệt.
Bước 1: Vẽ tam giác bên trên một tờ giấy má hoặc bên trên một ứng dụng hình đồ họa.
Bước 2: Tìm lối cao cho từng cạnh của tam giác. Đường cao là đường thẳng liền mạch vuông góc với cạnh ứng và trải qua đỉnh của tam giác.
Bước 3: Tìm nút giao của tía lối cao. Điểm này đó là trực tâm của tam giác.
Lưu ý: Nếu tam giác là tam giác vuông, thì trực tâm là vấn đề nằm tại đỉnh góc vuông.
Hy vọng vấn đề này tiếp tục giúp cho bạn đo lường và tính toán được trực tâm của tam giác một cơ hội đúng chuẩn.

Có, góc nhọn nhập tam giác sở hữu trực tâm.
Để nắm rõ rộng lớn về định nghĩa trực tâm, tất cả chúng ta nên biết trước đó về lối cao nhập tam giác. Đường cao nhập một tam giác là đoạn trực tiếp liên kết một đỉnh của tam giác với đối lập của chính nó và vuông góc với cạnh đối lập đỉnh bại liệt. Tam giác sở hữu tía lối cao, lối cao ứng với từng đỉnh.
Trực tâm của một tam giác là vấn đề phó của tía lối cao nhập tam giác bại liệt. Nghĩa là đó là điểm trùng với phó điểm của tía lối cao. Trực tâm hoàn toàn có thể được xác lập bằng phương pháp vẽ lối cao ứng cho từng cạnh của tam giác, tiếp sau đó nối những nút giao nhau của những lối cao cùng nhau. Điểm phó của những lối cao này đó là trực tâm của tam giác.
Vậy, với cùng 1 góc nhọn nhập tam giác, tao hoàn toàn có thể xác lập trực tâm của tam giác bằng phương pháp vẽ những lối cao ứng với từng cạnh.

Trực tâm là vấn đề phó của tía lối cao nhập tam giác. Đường cao nhập tam giác là đoạn trực tiếp liên kết một đỉnh của tam giác với đối lập của chính nó sao cho tới tạo ra trở thành một góc vuông.
Trực tâm sở hữu tầm quan trọng cần thiết nhập tam giác vì như thế nó được xem như là \"trung tâm\" của tam giác. Dưới đó là một vài lí tự vì như thế sao trực tâm sở hữu tầm quan trọng quan liêu trọng:
1. Tọa độ: Trực tâm hoàn toàn có thể được dùng nhằm xác lập tọa phỏng của tam giác bên trên mặt mũi phẳng lặng. Khi biết những tọa phỏng của tía đỉnh của tam giác, tao hoàn toàn có thể đơn giản và dễ dàng đo lường và tính toán tọa phỏng của trực tâm trải qua công thức tầm.
2. Đường trung trực: Trực tâm cũng là vấn đề bên trên lối trung trực của những cạnh của tam giác. Đường trung trực là đường thẳng liền mạch trải qua trung điểm của từng cạnh và vuông góc với cạnh bại liệt. Trực tâm phía trên lối trung trực của từng cạnh, điều này được cho phép tao xác lập một đường thẳng liền mạch độc nhất trải qua trực tâm và vuông góc với từng cạnh.
3. Giao điểm của tía lối cao: Trực tâm là vấn đề bên trên lối cao của từng cạnh. Đường cao là đoạn trực tiếp từ là 1 đỉnh của tam giác cho tới đối lập của chính nó và tạo ra trở thành góc vuông. Trực tâm là vấn đề phó của tía lối cao, vậy nên nó sở hữu tầm quan trọng cần thiết trong những việc xác lập những lối cao và quan hệ thân ái bọn chúng.
4. Tính đối xứng: Trực tâm cũng là vấn đề đối xứng của những đỉnh của tam giác qua loa trung điểm của cạnh ứng. Vấn đề này Có nghĩa là nếu như tao vẽ những đường thẳng liền mạch kể từ trực tâm cho tới những đỉnh của tam giác, thì những đoạn trực tiếp này tiếp tục hạn chế nhau ở một điểm độc nhất và tạo ra trở thành những góc đồng hóa.
Như vậy, trực tâm sở hữu tầm quan trọng cần thiết nhập tam giác cũng chính vì nó không những canh ty xác lập tọa phỏng và quan hệ Một trong những lối cao, mà còn phải tương quan cho tới những lối trung trực và đặc điểm đối xứng của tam giác.

Xem thêm: trường đại học kỹ thuật công nghiệp

Ba lối cao của tam giác gặp gỡ nhau bên trên một điểm gọi là trực tâm của tam giác. Trực tâm là vấn đề phó của tía lối cao nhập tam giác. Đường cao nhập tam giác được xác lập bằng phương pháp vẽ từ là 1 đỉnh của tam giác vuông góc với cạnh đối lập. Do bại liệt, nhằm lần trực tâm của tam giác, tao cần thiết xác lập lối cao của tam giác và lần nút giao của bọn chúng.

Trực tâm của tam giác là vấn đề phó của tía lối cao nhập tam giác bại liệt. Đường cao nhập tam giác là đoạn trực tiếp liên kết một đỉnh của tam giác với cạnh đối lập sao cho tới tạo ra trở thành một góc vuông.
Điểm nhằm xác lập trực tâm của tam giác nên biết rằng tam giác cân nặng sở hữu hai tuyến phố cao đồng lâu năm. Nguyên tắc chủ yếu nhằm xác lập trực tâm của tam giác cân nặng là phó điểm của những lối cao bại liệt. Vì hai tuyến phố cao trùng nhau và sở hữu nằm trong phỏng lâu năm, nên trực tâm của tam giác cân nặng nằm tại thân ái trực tiếp nối nhị đỉnh lòng.
Ví dụ, cho tới tam giác ABC với AB = AC. Đường cao kể từ đỉnh A sẽ tạo nên trở thành góc vuông với BC. Điểm phó của lối cao này với BC là trực tâm của tam giác.
Tuy nhiên, nhằm chắc hẳn rằng rằng tam giác cân nặng sở hữu trực tâm, tao nên biết rằng tam giác bại liệt thực sự cân nặng. Tam giác cân nặng là tam giác sở hữu nhị cạnh cân nhau. Nếu tam giác ko cân nặng, không tồn tại trực tâm.
Tóm lại, tam giác cân nặng hoàn toàn có thể sở hữu trực tâm, tuy nhiên ko cần toàn bộ những tam giác cân nặng đều phải có trực tâm. Để xác lập trực tâm của tam giác cân nặng, cần thiết kiểm tra sự bằng phẳng Một trong những cạnh và góc nhập tam giác.

Trong hình học tập, một tam giác hoàn toàn có thể không tồn tại trực tâm. Để hiểu điều này, tất cả chúng ta nên biết rằng trực tâm của một tam giác là vấn đề phó của tía lối cao nhập tam giác bại liệt. Đường cao nhập tam giác là những đoạn trực tiếp được kéo kể từ từng đỉnh của tam giác cho tới đối lập của chính nó và tạo ra trở thành một góc vuông.
Tuy nhiên, nhập một vài tình huống đặc biệt quan trọng, tam giác hoàn toàn có thể không tồn tại lối cao, tức là không tồn tại đoạn trực tiếp này kéo từ là 1 đỉnh của tam giác cho tới cạnh đối lập và tạo ra trở thành một góc vuông. Khi bại liệt, tam giác này sẽ không tồn tại trực tâm.
Ví dụ, nhập tình huống tam giác cân nặng, toàn bộ những lối cao của tam giác đều trùng với những cạnh và không tồn tại phó điểm. Do bại liệt, tam giác cân nặng tiếp tục không tồn tại trực tâm.
Tuy nhiên, hầu hết tam giác thường thì đều phải có trực tâm, vì như thế từng tam giác đều hoàn toàn có thể vẽ được tối thiểu một lối cao và những lối cao này đều hạn chế nhau bên trên một điểm độc nhất, điểm này được gọi là trực tâm.
Tóm lại, nhập hình học tập, tam giác hoàn toàn có thể không tồn tại trực tâm nếu như không tồn tại lối cao tồn bên trên, tuy nhiên hầu hết tam giác đều phải có trực tâm trải qua nút giao của tía lối cao.

Trực tâm và tâm nước ngoài tiếp là nhị định nghĩa không giống nhau nhập tam giác.
1. Trực tâm của tam giác là vấn đề trùng với phó điểm của tía lối cao nhập tam giác bại liệt. Đường cao nhập tam giác là đoạn trực tiếp liên kết một đỉnh của tam giác cho tới cạnh đối lập và vuông góc với cạnh bại liệt.
2. Tâm nước ngoài tiếp của tam giác là vấn đề trùng với tâm của lối tròn trặn nước ngoài tiếp tam giác bại liệt. Đường tròn trặn nước ngoài tiếp tam giác là lối tròn trặn trải qua tía đỉnh của tam giác.
Vì vậy, trực tâm và tâm nước ngoài tiếp của tam giác là nhị điểm không giống nhau và rất khác nhau.
Để nắm rõ rộng lớn, tao hoàn toàn có thể vận dụng công thức tính trực tâm và tâm nước ngoài tiếp cho 1 tam giác rõ ràng.

Tam giác không tồn tại trực tâm Khi tía lối cao của tam giác ko hạn chế nhau bên trên một điểm độc nhất. Vấn đề này xẩy ra Khi tam giác là tam giác cân nặng hoặc tam giác vuông.
- Trong tam giác cân nặng, hai tuyến phố cao hạn chế nhau bên trên trung điểm của cạnh lòng, ko trải qua đỉnh tam giác. Do bại liệt, tam giác cân nặng không tồn tại trực tâm.
- Trong tam giác vuông, một lối cao là cạnh huyền, còn hai tuyến phố cao hạn chế nhau bên trên đỉnh góc vuông. Do bại liệt, tam giác vuông không tồn tại trực tâm.
Trên thực tiễn, tam giác không tồn tại trực tâm là tình huống đặc biệt quan trọng, và đa số những tam giác không giống đều phải có trực tâm là vấn đề phó của tía lối cao.

Đường trực tiếp trung trực của một cạnh tam giác ko trải qua trực tâm.
Trực tâm của một tam giác là vấn đề phó của tía lối cao nhập tam giác bại liệt. Đường cao là đường thẳng liền mạch nối một đỉnh của tam giác với đối lập của chính nó sao cho tới tạo ra trở thành một góc vuông.
Đường trực tiếp trung trực của một cạnh tam giác là đường thẳng liền mạch trải qua trung điểm của cạnh bại liệt và vuông góc với cạnh bại liệt. Đường trực tiếp trung trực ko trải qua trực tâm vì như thế trực tâm là vấn đề phó của tía lối cao, ko cần là trung điểm của cạnh tam giác.
Vì vậy, đường thẳng liền mạch trung trực của một cạnh tam giác ko trải qua trực tâm.

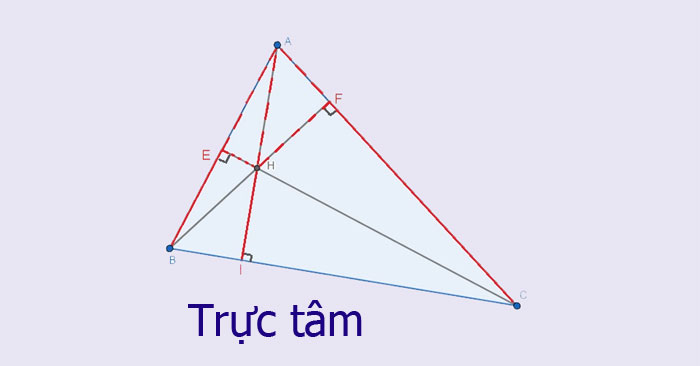
Xem thêm: cách mạng công nghiệp lần 3

Điểm trùng điểm trực tâm nhập tam giác là vấn đề trùng với điểm trực tâm, tức là vấn đề phó của tía lối cao nhập tam giác.
Đường cao nhập tam giác là đoạn trực tiếp liên kết một đỉnh của tam giác với đối lập của chính nó sao cho tới tạo ra trở thành một góc vuông.
Để lần điểm trực tâm của tam giác và điểm trùng điểm trực tâm, tao hoàn toàn có thể tuân theo công việc sau:
1. Vẽ tam giác ABC với những đỉnh ứng là A, B và C.
2. Vẽ lối cao kẻ kể từ từng đỉnh của tam giác cho tới đối lập của chính nó. Đường cao AB là đoạn trực tiếp liên kết đỉnh A với đối lập của chính nó bên trên cạnh BC. Tương tự động, vẽ lối cao BC và lối cao AC.
3. Tìm phó điểm của tía lối cao là vấn đề trực tâm của tam giác. Điểm này được kí hiệu là H.
4. Kiểm tra coi điểm H sở hữu trùng với cùng 1 điểm này bại liệt không giống nhập tam giác hay là không. Nếu sở hữu, điểm bại liệt là vấn đề trùng điểm trực tâm.
Với công việc bên trên, tao hoàn toàn có thể tìm kiếm ra điểm trực tâm và đánh giá coi nó sở hữu trùng với cùng 1 điểm không giống nhập tam giác hay là không.

Trục tâm và trực tâm nhập tam giác sở hữu một mối liên hệ đặc biệt quan trọng.
- Trục tâm là vấn đề phó của tía lối trung tuyến nhập tam giác. Đường trung tuyến là đoạn trực tiếp liên kết trung điểm của nhị đỉnh với đỉnh không được nối.
- Trực tâm là vấn đề phó của tía lối cao nhập tam giác. Đường cao nhập tam giác là đoạn trực tiếp liên kết một đỉnh cho tới cạnh đối lập sao cho tới tạo ra trở thành góc vuông.
- Trực tâm của tam giác trực thuộc tam giác nếu như tam giác ko cần là tam giác vuông.
- Nếu tam giác là tam giác vuông, trực tâm ko trực thuộc tam giác tuy nhiên ở ngoài tam giác, cơ hội những đỉnh tam giác một khoảng chừng tự nửa đường kính của lối tròn trặn nội tiếp tam giác.
Tóm lại, trục tâm và trực tâm của tam giác sở hữu mối liên hệ riêng không liên quan gì đến nhau. Trực tâm là vấn đề phó của tía lối cao nhập tam giác, trong những lúc trục tâm là vấn đề phó của tía lối trung tuyến nhập tam giác.