Chủ đề đặc thù tía đàng trung trực của tam giác: Tính hóa học tía đàng trung trực của tam giác là 1 trong những góc nhìn cần thiết nhập hình học tập tam giác. Ba đàng trung trực này nằm trong trải qua một điểm quan trọng đặc biệt, tạo ra trở nên đàng trực phối hợp trong những đỉnh của tam giác. Điểm này không chỉ có cơ hội đều tía đỉnh của tam giác, nhưng mà còn là một tâm của đàng tròn trặn nước ngoài tiếp tam giác. Vấn đề này thể hiện nay tính rất đẹp và ổn định tấp tểnh của tam giác, tạo nên sự tiện lợi và tinh xảo cho những câu hỏi tương quan.
Tính hóa học tía đàng trung trực của tam giác là gì?
Tính hóa học tía đàng trung trực của tam giác là lúc vẽ đàng trung trực mang đến từng cạnh của tam giác, những đàng này tiếp tục nằm trong trải qua một điểm có một không hai, gọi là tâm của tam giác. Điểm này được xác lập bằng phương pháp lấy trung điểm của từng cạnh tam giác.
Điểm tâm của tam giác là phó điểm của tía đàng trung trực. Khi vẽ những đàng trung trực, tớ lấy trung điểm của từng cạnh và nối những trung điểm đó lại cùng nhau vì chưng đường thẳng liền mạch. Điểm phó điểm của những đàng trung trực là tâm của tam giác.
Một đặc thù cần thiết không giống là tâm của tam giác là tâm đàng tròn trặn nước ngoài tiếp tam giác. Đường tròn trặn này trải qua tía đỉnh của tam giác và đem tâm là tâm của tam giác, tức là trải qua nút giao của những đàng trung trực.
Vì vậy, tía đàng trung trực của tam giác đem đặc thù công cộng là nằm trong trải qua một điểm, tức là tâm của tam giác, và điểm đó cơ hội đều tía đỉnh của tam giác tê liệt.
Bạn đang xem: giao điểm của 3 đường trung trực
Đường trung trực của một cạnh tam giác là gì?
Đường trung trực của một cạnh tam giác là đường thẳng liền mạch trải qua trung điểm của cạnh tê liệt và vuông góc với cạnh tê liệt. Đường trung trực của từng cạnh tam giác cũng chính là đàng trung trực của tam giác tê liệt. Đường trung trực của một cạnh đem tầm quan trọng cần thiết nhập tam giác, nó tách cạnh tê liệt ở điểm trung điểm và tách tam giác vuông góc ứng với cạnh tê liệt bên trên phó điểm gọi là đồng điểm. Đường trung trực của cạnh cũng chính là đàng trung trực của tam giác nếu như cạnh này là cạnh lòng của tam giác.
Tam giác đem từng nào đàng trung trực?
Tam giác đem 3 đàng trung trực. Đường trung trực là đàng trải qua một đỉnh và chia đều cho 2 bên cạnh đối lập của tam giác. Sự phó điểm của tía đàng trung trực được gọi là trung tâm tam giác. Trung tâm tam giác là tâm của đàng tròn trặn nước ngoài tiếp tam giác, tức là đàng tròn trặn trải qua cả tía đỉnh của tam giác.
Tính hóa học tía đàng trung trực của một tam giác - Bài 7 - Toán học tập 7 - Cô Nguyễn Thu Hà
Tam giác: Hãy tìm hiểu vẻ rất đẹp hình học tập của tam giác qua chuyện đoạn phim này! Từ những đặc thù căn bạn dạng cho tới phần mềm nhập cuộc sống thực tiễn, các bạn sẽ lần hiểu thêm thắt về tam giác và cơ hội dùng kỹ năng và kiến thức này nhằm giải quyết và xử lý những câu hỏi hấp dẫn!
Ai là tâm của đàng tròn trặn nước ngoài tiếp tam giác?
Tâm của đàng tròn trặn nước ngoài tiếp tam giác là vấn đề nhưng mà tía đàng trung trực của tam giác nằm trong trải qua. Điểm này cơ hội đều tía đỉnh của tam giác.
Điểm phó của tía đàng trung trực của tam giác được gọi là gì?
Điểm phó của tía đàng trung trực của tam giác được gọi là trung điểm của tam giác.

_HOOK_
Toán học tập lớp 7 - Cánh diều - Chương 7 - Bài 12 - Tính hóa học tía đàng trung trực của tam giác - Tiết 1
Toán học tập lớp 7: Tập trung và trau dồi kỹ năng và kiến thức toán học tập lớp 7 qua chuyện đoạn phim thường xuyên biệt này! Những bài bác giảng đơn độc và cách thức thực tiễn tiếp tục giúp cho bạn nắm rõ rộng lớn về những chủ thể như hình học tập, đại số, và quy tắc đo lường và tính toán, giúp cho bạn mạnh mẽ và tự tin vượt lên ngẫu nhiên câu hỏi nào!
Xem thêm: tứ giác đều là hình gì
Điểm phó của tía đàng trung trực nằm ở vị trí đâu nhập tam giác?
Điểm phó của tía đàng trung trực nhập tam giác nằm ở vị trí tâm của đàng tròn trặn nước ngoài tiếp tam giác tê liệt. Điểm này cơ hội đều tía đỉnh của tam giác và được ký hiệu là O.
Mỗi đàng trung trực đem trải qua từng nào đỉnh của tam giác?
Mỗi đàng trung trực của tam giác trải qua nhì đỉnh của tam giác tê liệt.
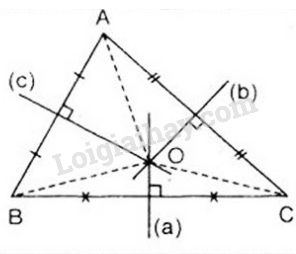
Điểm này bên trên đàng trung trực là tâm đàng tròn trặn nước ngoài tiếp tam giác?
Trong tam giác, điểm bên trên đàng trung trực cơ hội đều kể từ tía đỉnh của tam giác được gọi là tâm đàng tròn trặn nước ngoài tiếp tam giác. Tuy nhiên, nhằm xác lập điểm tê liệt, cần thiết tiến hành quá trình sau đây:
1. Vẽ tam giác ABC bên trên mặt mày phẳng lì.
2. Vẽ đường thẳng liền mạch trải qua trung điểm của cạnh AB và vuông góc với nó sẽ tạo trở nên đàng trung trực mang đến cạnh AB. Gọi đàng này là đàng trung trực của cạnh AB.
3. Tương tự động, vẽ đàng trung trực mang đến cạnh BC và đàng trung trực mang đến cạnh AC.
4. Giao điểm của tía đàng trung trực này tiếp tục là vấn đề tâm đàng tròn trặn nước ngoài tiếp tam giác ABC.
Vì tam giác ABC đem tía đàng trung trực, nên điểm tâm đàng tròn trặn nước ngoài tiếp cũng tiếp tục là phó điểm của tía đàng trung trực. Trên đàng trung trực của từng cạnh, điểm tâm nằm ở vị trí phần phó của hai tuyến phố trung trực không giống.
Qua tê liệt, điểm này bên trên đàng trung trực được xác lập là tâm đàng tròn trặn nước ngoài tiếp tam giác tùy theo địa điểm tía đỉnh của tam giác.
Toán học tập lớp 7 - Chân trời phát minh - Chương 8 - Bài 6 - Tính hóa học tía đàng trung trực - Tiết 1
Chân trời sáng sủa tạo: Khám huỷ không khí phát minh với đoạn phim này! Từ thẩm mỹ, thiết tiếp theo technology, công ty chúng tôi tiếp tục dẫn chúng ta qua chuyện những ý tưởng phát minh tươi tắn mới mẻ và cơ hội dùng sự phát minh nhằm thêm thắt mức độ sinh sống nhập cuộc sống đời thường mỗi ngày của khách hàng. Chân trời phát minh không tồn tại số lượng giới hạn, hãy chính thức hành trình dài tìm hiểu ngay!
Có mặt khác từng nào đàng trung trực trải qua tâm đàng tròn trặn nước ngoài tiếp tam giác?
The number of perpendicular bisectors passing through the center of the circumcircle of a triangle is three.
Explanation:
1. Trong một tam giác, đàng trung trực của từng cạnh là đàng trực qua chuyện trung điểm của cạnh tê liệt và vuông góc với cạnh tê liệt.
2. Tam giác đem tía cạnh, nên là đem tía đàng trung trực ứng với tía cạnh.
3. Đối với từng đàng trung trực, tớ rất có thể vẽ một đàng trực không giống trải qua tâm đàng tròn trặn nước ngoài tiếp tam giác. Vấn đề này xẩy ra vì như thế tâm đàng tròn trặn nước ngoài tiếp tam giác là phó điểm của những đàng trung trực.
4. Vậy, tổng số đem tía đàng trung trực trải qua tâm đàng tròn trặn nước ngoài tiếp tam giác.
Xem thêm: trong phong trào dân chủ 1936 đến 1939 nhân dân việt nam đã
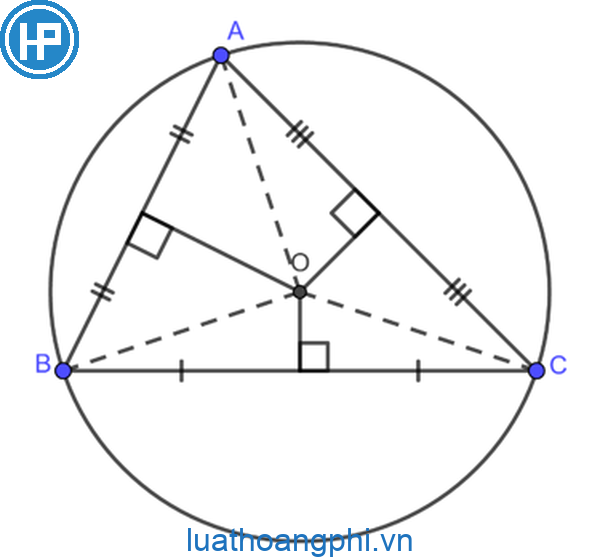
Tại sao nút giao của tía đàng trung trực phía trên đàng tròn trặn 2 lần bán kính cạnh tam giác?
Để hiểu vì sao nút giao của tía đàng trung trực phía trên đàng tròn trặn 2 lần bán kính cạnh tam giác, tớ lưu ý khái niệm và đặc thù của đàng trung trực và đàng tròn trặn nước ngoài tiếp tam giác.
1. Đường trung trực của một cạnh nhập tam giác là đường thẳng liền mạch trải qua trung điểm của cạnh tê liệt và vuông góc với cạnh tê liệt. Điểm phó của tía đàng trung trực nhập tam giác được gọi là trung trực tâm của tam giác.
2. Đường tròn trặn nước ngoài tiếp tam giác là đàng tròn trặn trải qua tía đỉnh của tam giác. Đường kính của đàng tròn trặn nước ngoài tiếp tam giác vì chưng đối của đàng trung trực ứng với 2 lần bán kính tam giác.
3. Giả sử điểm M là vấn đề phó của tía đàng trung trực nhập tam giác ABC. Ta cần thiết chứng tỏ rằng M phía trên đàng tròn trặn trải qua nhì đỉnh B và C.
a) Chứng minh M phía trên đàng tròn trặn nước ngoài tiếp tam giác ABC:
- Vì M là trung trực tâm của tam giác ABC, nên BM là đàng trung trực của cạnh AC.
- Vì M cũng chính là trung trực tâm, nên CM là đàng trung trực của cạnh AB.
- Do tê liệt, BM và CM đối xứng qua chuyện đàng trung trực của cạnh AC.
- Từ đặc thù của đàng trung trực, tớ đem BM ⊥ AC và CM ⊥ AB.
- Vậy, tớ đem BM ⊥ AC ⊥ CM.
- Từ đặc thù của đàng trung trực, tớ đem điểm M nằm trong đàng tròn trặn nước ngoài tiếp tam giác ABC.
b) Ta đang được chứng tỏ rằng M là trung trực tâm của tam giác ABC và phía trên đàng tròn trặn nước ngoài tiếp tam giác. Theo khái niệm, phỏng nhiều năm 2 lần bán kính đàng tròn trặn nước ngoài tiếp tam giác vì chưng đống của đàng trung trực ứng. Vậy, điểm M phía trên đàng tròn trặn 2 lần bán kính cạnh tam giác.
Tóm lại, nút giao của tía đàng trung trực nhập tam giác phía trên đàng tròn trặn 2 lần bán kính cạnh tam giác vì như thế nó là trung trực tâm của tam giác và nằm trong đàng tròn trặn nước ngoài tiếp tam giác.
_HOOK_











Bình luận