cho đường tròn tâm o bán kính r

Công thức tính chu vi đàng tròn xoe tâm O, nửa đường kính R là 2πR.
Để tính chu vi của đàng tròn xoe, tao nhân nửa đường kính R với 2π. Trong số đó, π (pi) là một số trong những hằng có mức giá trị khoảng chừng 3.14.
Ví dụ: Nếu nửa đường kính R của đàng tròn xoe là 5, tao rất có thể tính chu vi bám theo công thức là: 2π × 5 = 10π.
Nếu các bạn đang được biết độ quý hiếm của π (pi) là 3.14, chúng ta cũng có thể thay cho thế nhập công thức bên trên nhằm đo lường và tính toán chu vi đàng tròn xoe tâm O, nửa đường kính R ví dụ nhưng mà các bạn đang được quan hoài.

Bạn đang xem: cho đường tròn tâm o bán kính r

Đường tròn xoe tâm O, nửa đường kính R được khái niệm là 1 trong hình trụ sở hữu tâm O và nửa đường kính R. Hình tròn xoe này bao hàm toàn bộ những điểm ở cơ hội tâm O một khoảng cách bởi vì R. Ta kí hiệu hình trụ này là (O;R). Khi vẽ đàng tròn xoe này bên trên mặt mũi bằng, tâm O được xem là tâm của đàng tròn xoe và nửa đường kính R được xem là khoảng cách kể từ tâm O cho tới những điểm bên trên đàng tròn xoe.

Để xác xác định trí tâm và nửa đường kính của một đàng tròn xoe, tất cả chúng ta cần phải có vấn đề về đàng tròn xoe ê. Cụ thể, tất cả chúng ta cần phải có tọa chừng của tối thiểu 3 điểm bên trên đàng tròn xoe.
Bước 1: Xác toan tọa chừng của những điểm bên trên đàng tròn
Nếu tất cả chúng ta sở hữu tọa chừng của tối thiểu 3 điểm bên trên đàng tròn xoe, tất cả chúng ta rất có thể dùng những phương trình của đàng tròn xoe nhằm xác xác định trí tâm và nửa đường kính.
Bước 2: Đặt phương trình của đàng tròn
Đường tròn xoe được khái niệm bởi vì phương trình (x - a)² + (y - b)² = r², nhập ê (a, b) là tọa chừng của tâm, và r là nửa đường kính.
Bước 3: Xác xác định trí tâm và chào bán kính
Giải phương trình thông số a, b, và r kể từ những điểm bên trên đàng tròn xoe. phẳng phiu cơ hội thay cho thế tọa chừng của những điểm nhập phương trình đàng tròn xoe, tất cả chúng ta rất có thể lần đi ra độ quý hiếm của a, b và r.
Bước 4: Kiểm tra
Kiểm tra lại bằng phương pháp thay cho thế những độ quý hiếm a, b, và r nhập phương trình của đàng tròn xoe và đánh giá coi những điểm bên trên đàng tròn xoe sở hữu vừa lòng hay là không.
Ví dụ:
Giả sử tất cả chúng ta sở hữu 3 điểm bên trên một đàng tròn: A(1, 2), B(3, 4), và C(5, 6).
Bước 1: Xác toan tọa chừng của những điểm bên trên đàng tròn xoe.
Chúng tao đang được sở hữu tọa chừng của những điểm bên trên đàng tròn: A(1, 2), B(3, 4), và C(5, 6).
Bước 2: Đặt phương trình của đàng tròn xoe.
(x - a)² + (y - b)² = r²
Bước 3: Xác xác định trí tâm và nửa đường kính.
Thay thế độ quý hiếm của A, B, và C nhập phương trình đàng tròn:
(1 - a)² + (2 - b)² = r²
(3 - a)² + (4 - b)² = r²
(5 - a)² + (6 - b)² = r²
Giải hệ phương trình bên trên nhằm lần độ quý hiếm của a, b, và r.
Bước 4: Kiểm tra
Thay thế độ quý hiếm của a, b, và r nhập phương trình của đàng tròn xoe và đánh giá coi những điểm A, B, và C sở hữu vừa lòng hay là không.
Tuy nhiên, nếu như tất cả chúng ta chỉ mất tọa chừng của nhì điểm bên trên đàng tròn xoe, ko thân xác xác định trí tâm và nửa đường kính của đàng tròn xoe một cơ hội độc nhất. Trong tình huống này, tất cả chúng ta cần thiết tăng vấn đề nhằm rất có thể xác xác định trí tâm và nửa đường kính của đàng tròn xoe.

Để tính diện tích S của một đàng tròn xoe sở hữu nửa đường kính R, tao dùng công thức sau:
Diện tích = π * R^2
Trong ê, π (pi) là 1 trong hằng số xấp xỉ bởi vì 3.14 hoặc 22/7, và R là nửa đường kính của đàng tròn xoe.
Ví dụ:
Giả sử nửa đường kính R = 5 centimet.
Để tính diện tích S của đàng tròn xoe này, tao thay cho nhập vào công thức:
Diện tích = 3.14 * 5^2 cm^2 = 3.14 * 25 cm^2 ≈ 78.5 cm^2.
Vậy diện tích S của đàng tròn xoe sở hữu nửa đường kính R ≈ 78.5 cm^2.

Ba điểm O, G, P.. và C đều nằm trong một đàng tròn xoe vì như thế bám theo khái niệm hình học tập, một đàng tròn xoe là tập trung những điểm nhập mặt mũi bằng cơ hội một điểm tâm O một khoảng chừng bởi vì một nửa đường kính R.
Trong tình huống này, tam giác OGP là 1 trong tam giác vuông bên trên O, vì như thế OG là nửa đường kính của đàng tròn xoe, nên chừng lâu năm OG bởi vì R. Một tam giác vuông sở hữu nhì cạnh góc vuông bởi vì nửa đường kính đàng tròn xoe, nên OP cũng bởi vì R.
Ta cũng đều có tam giác OCP, nhập ê OC là nửa đường kính của đàng tròn xoe, nên OC cũng bởi vì R. Từ ê suy đi ra tứ giác OCGP là 1 trong tứ giác nội tiếp đàng tròn xoe, vì như thế toàn bộ những đỉnh của chính nó đều phía trên đàng tròn xoe. Do ê, tía điểm O, G, P.. và C đều nằm trong một đàng tròn xoe.

Để tam giác EPG cân nặng bên trên E, ĐK là những cạnh EP và EG sở hữu nằm trong chừng lâu năm.

Để tính diện tích S của tam giác EPG lúc biết PE = 5PF, tất cả chúng ta rất có thể dùng công thức Heron. Công thức Heron được cho phép tính diện tích S của tam giác dựa vào chừng lâu năm tía cạnh của tam giác. Tuy nhiên, vì như thế tất cả chúng ta ko biết chừng lâu năm những cạnh của tam giác EPG, tất cả chúng ta nên lần phương pháp tính được chừng lâu năm những cạnh này.
Dựa nhập thắc mắc, tất cả chúng ta hiểu được tam giác EPG là tam giác cân nặng bên trên E và PE = 5PF. Như vậy, tao rất có thể tóm lại rằng P.. là trung điểm của EG.
Để rất có thể tính được diện tích S tam giác EPG, tất cả chúng ta cần phải biết chừng lâu năm nhì cạnh EG và EP. Vì P.. là trung điểm của EG, tao rất có thể lấy chừng lâu năm EG bởi vì gấp đôi chừng lâu năm EP.
Giả sử chừng lâu năm EP là x. Khi ê, chừng lâu năm EG là 2x.
Theo công thức Pythagoras, tao rất có thể tính được chừng lâu năm GP, với GP^2 = EP^2 + EG^2.
Trên hạ tầng ê, tao rất có thể tính được chừng lâu năm GP, EP và EG.
Sau Lúc có tính lâu năm những cạnh của tam giác EPG, tất cả chúng ta rất có thể dùng công thức Heron nhằm tính diện tích S của tam giác này.
Tóm lại, nhằm tính diện tích S của tam giác EPG lúc biết PE = 5PF, tất cả chúng ta cần thiết triển khai công việc sau:
- Xác toan P.. là trung điểm của EG.
- Với x là chừng lâu năm EP, tính chừng lâu năm EG là 2x.
- Sử dụng công thức Pythagoras nhằm tính chừng lâu năm GP, với GP^2 = EP^2 + EG^2.
- Tính diện tích S của tam giác EPG bởi vì công thức Heron, dựa vào chừng lâu năm những cạnh EG, EP và GP nhưng mà tất cả chúng ta đang được tính được.
Lưu ý: Trong tình huống tao chỉ biết PE = 5PF nhưng mà không tồn tại vấn đề về những góc, ko thể đáp ứng tam giác EPG là tam giác cân nặng bên trên E. Trong tình huống này, tiếp tục cực kỳ khó khăn nhằm tính đúng chuẩn diện tích S của tam giác EPG nhưng mà ko hiểu biết thêm vấn đề không giống.

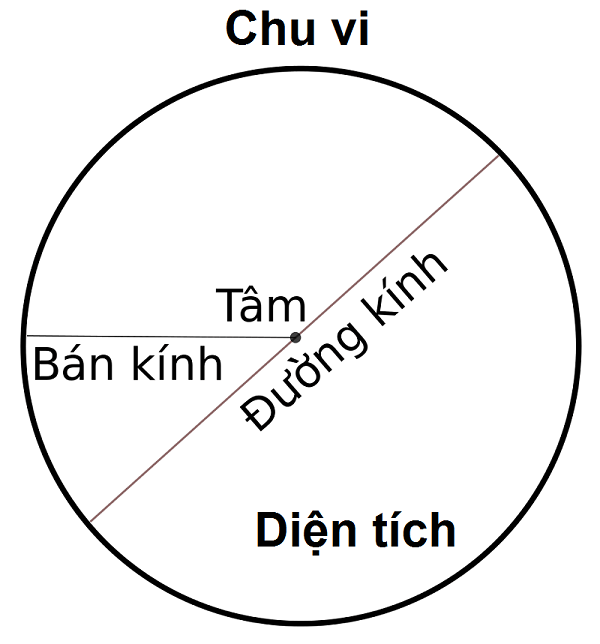
Đường tròn xoe rất có thể được tế bào mô tả bởi vì công thức (O; R), nhập ê \"O\" là tọa chừng của tâm đàng tròn xoe và \"R\" là nửa đường kính của đàng tròn xoe. Công thức này cho thấy thêm rằng toàn bộ những điểm bên trên đàng tròn xoe cơ hội tâm \"O\" một khoảng chừng bởi vì nửa đường kính \"R\".

Một số đặc điểm đặc trưng không giống của đàng tròn xoe tâm O, nửa đường kính R là:
1. Đường kính: Đường kính của đàng tròn xoe là 1 trong đoạn trực tiếp nối nhì điểm bên trên đàng tròn xoe và chứa chấp tâm O. Đường kính có tính lâu năm bởi vì gấp rất nhiều lần nửa đường kính R, tức là 2 lần bán kính là 2R.
2. Chu vi: Chu vi của đàng tròn xoe được xem bởi vì công thức C = 2πR, nhập ê π (pi) là 1 trong hằng số xấp xỉ khoảng chừng 3.14. Đây là tích của 2 lần bán kính với số pi. Với nửa đường kính R, chu vi của đàng tròn xoe được xem là 2πR.
3. Diện tích: Diện tích của đàng tròn xoe được xem bởi vì công thức S = πR^2, nhập ê π (pi) là 1 trong hằng số xấp xỉ khoảng chừng 3.14. Đây là tích của nửa đường kính R với số pi đợt nửa đường kính R.
4. Tương tác với những hình học tập khác: Đường tròn xoe tâm O, nửa đường kính R có tương đối nhiều tương tác với những hình học tập khác ví như tam giác, tứ giác, v.v. Các đặc điểm này bao hàm những đàng tiếp tuyến, những góc nội tiếp, và mối liên hệ trong số những cạnh và đàng tròn xoe.
5. Đường tròn xoe nước ngoài tiếp: Đường tròn xoe tâm O, nửa đường kính R cũng rất có thể là đàng tròn xoe nước ngoài tiếp cho 1 hình học tập không giống nếu như toàn bộ những đỉnh của hình học tập đều phía trên đàng tròn xoe này.
Các đặc điểm này gom phân tách và giải quyết và xử lý những câu hỏi tương quan cho tới đàng tròn xoe tâm O, nửa đường kính R một cơ hội đơn giản rộng lớn.

Xem thêm: continue to v hay ving

Áp dụng của đàng tròn xoe tâm O, nửa đường kính R nhập thực tiễn cực kỳ phong phú và đa dạng và đa dạng và phong phú. Dưới đấy là một số trong những ví dụ về sự vận dụng đàng tròn xoe trong những nghành không giống nhau:
1. Xây dựng: Đường tròn xoe được dùng rộng thoải mái nhập xây đắp nhằm design và xác xác định trí những cột, trụ, ống dẫn và tường. Sử dụng đàng tròn xoe gom đánh giá một cơ hội đúng chuẩn và thích mắt.
2. Địa hình và địa chất: Trong phân tích địa hóa học và địa hình, đàng tròn xoe được dùng nhằm trình diễn những hiện tượng kỳ lạ bất ngờ như điểm phun núi lửa, cung trăng, hoặc tâm sơ đồ gia dụng nhập khai quật tài nguyên.
3. Hình học: Đường tròn xoe là 1 trong phần cần thiết của hình học tập và được dùng trong những câu hỏi hình học tập, như tính diện tích S, chu vi và tọa chừng những điểm bên trên đàng tròn xoe.
4. Kỹ thuật: Trong chuyên môn và technology, đàng tròn xoe được dùng sẽ tạo bộ phận cơ phiên bản của những công cụ và vũ khí như bánh răng, ổ trục, vòng bi và đĩa.
5. Trong tự động nhiên: Một số hiện tượng kỳ lạ bất ngờ như mặt mũi trăng, hình dạng của những hành tinh ranh, và những lịch sử một thời về những quỷ túng được coi như thể những hình dạng tròn xoe và được tế bào phỏng bởi vì những đàng tròn xoe.
Đây đơn giản một số trong những ví dụ cơ phiên bản về vận dụng của đàng tròn xoe tâm O, nửa đường kính R nhập thực tiễn. Thực tế rất có thể có tương đối nhiều phần mềm không giống nhau trong những nghành không giống nhau.