Chủ đề thể tích bát diện đều: Thể tích chén bát diện đều là định nghĩa đặc biệt thú vị nhập toán học tập. Nó thể hiện nay năng lực đo lường và tính toán và xác lập thể tích của một khối hình đặc trưng. Thông qua loa công thức V=2V1=2.a3, tớ rất có thể đơn giản dễ dàng đo lường và tính toán thể tích của khối chén bát diện đều. Đây là 1 trong những chủ thể thú vị nhằm tìm hiểu hiểu và vận dụng nhập thực tiễn.
Tìm công thức tính thể tích của khối chén bát diện đều.
Để tính thể tích của khối chén bát diện đều, tớ dùng công thức sau:
V = 2V1 = 2 * a^3
Trong cơ,
- V là thể tích của khối chén bát diện đều,
- V1 là thể tích của một phía bằng chén bát diện đều,
- a là phỏng nhiều năm cạnh của mặt mũi bằng chén bát diện đều.
Công thức bên trên rất có thể được minh chứng bằng phương pháp phân tách khối chén bát diện đều trở thành những mặt mũi bằng chén bát diện riêng không liên quan gì đến nhau, từng mặt mũi bằng rất có thể tích là a^2, tiếp sau đó tính tổng thể tích của những mặt mũi bằng này.
Ví dụ: Nếu cạnh của mặt mũi bằng chén bát diện đều là 3 đơn vị chức năng, thì thể tích của khối chén bát diện đều là:
V = 2 * (3^3) = 54 đơn vị chức năng thể tích.
Bạn đang xem: thể tích bát diện đều

Khái niệm chén bát diện đều là gì?
Bát diện đều là 1 trong những khối hình bao gồm 8 mặt mũi đều phải có diện tích S cân nhau và những cạnh tuy nhiên song và cân nhau. phẳng cơ hội hạn chế một khối vuông đều theo gót đàng chéo cánh của mặt mũi đỉnh, tớ rất có thể dẫn đến một chén bát diện đều.
Thể tích của một chén bát diện đều rất có thể được xem vì chưng công thức V = 2V1, nhập cơ V1 là thể tích của khối vuông đều ban sơ. Tức là thể tích của khối chén bát diện đều là gấp hai thể tích của khối vuông đều nằm trong cạnh.
Công thức tính thể tích khối chén bát diện đều nhập không khí 3 chiều là gì?
Công thức tính thể tích khối chén bát diện đều nhập không khí 3 chiều được xem vì chưng công thức V = 2V1 = 2.a^3. Trong số đó, V là thể tích khối chén bát diện đều, V1 là thể tích của chén bát diện đều cạnh a, và a là phỏng nhiều năm cạnh của chén bát diện đều.
Thể tích chén bát diện đều
Đã khi nào các bạn tò mò mẫm về thể tích của một chén bát diện đều chưa? Hãy coi đoạn phim này nhằm mày mò công thức và phương pháp tính thể tích của một chén bát diện đều thích mắt và đơn giản và giản dị nhé!
Làm thế này nhằm tính được thể tích khối chén bát diện đều lúc biết cạnh của nó?
Để tính thể tích của khối chén bát diện đều lúc biết cạnh của chính nó, tớ dùng công thức:
V = 2 * V1 = 2 * a^3
Trong cơ, a là cạnh của khối.
Bước 1: sành cạnh a của khối chén bát diện đều
Bước 2: Tính thể tích một chén bát diện đều V1 = a^3
Bước 3: Nhân thể tích vừa phải tính được với 2 nhằm tìm hiểu thể tích khối chén bát diện đều V
Ví dụ:
Giả sử tớ sở hữu một khối chén bát diện đều phải có cạnh a = 5 centimet.
Bước 1: a = 5 cm
Bước 2: Tính thể tích V1 = a^3 = 5^3 = 125 cm^3
Bước 3: Tính thể tích khối chén bát diện đều V = 2 * V1 = 2 * 125 = 250 cm^3
Vậy thể tích của khối chén bát diện đều phải có cạnh 5 centimet là 250 cm^3.
Trình bày tiến độ tính thể tích khối chén bát diện đều?
Để tính thể tích khối chén bát diện đều, tớ cần thiết thực hiện như sau:
Bước 1: Xác lăm le phỏng nhiều năm cạnh (a) của khối chén bát diện đều.
Bước 2: Tính diện tích S chén bát diện đều (A) vì chưng công thức: A = (3√3/2) * a^2.
Bước 3: Tính thể tích khối chén bát diện đều (V) vì chưng công thức: V = 2 * A.
Vậy tiến độ tính thể tích khối chén bát diện đều được tiến hành bằng phương pháp xác lập phỏng nhiều năm cạnh và vận dụng những công thức tính diện tích S và thể tích ứng.
_HOOK_
Xem thêm: trường đại học công nghệ và quản lý hữu nghị
Giải bài xích tập dượt 2 trang 25 SGK Hình học tập 12 Tính thể tích khối chén bát diện đều cạnh a
Các bài xích tập dượt hình học tập lớp 12 rất có thể khiến cho các bạn cảm nhận thấy khó khăn khăn? Đừng lo phiền, đoạn phim này tiếp tục khiến cho bạn giải từng bài xích tập dượt hình học tập 12 một cơ hội đơn giản dễ dàng và thông minh! Đừng vứt lỡ!
Tại sao thể tích khối chén bát diện đều được xem vì chưng công thức 2V1?
Thể tích khối chén bát diện đều được xem vì chưng công thức 2V1 vì thế chén bát diện đều phải có nhì chén bát lòng đều và từng chén bát lòng rất có thể tích là V1. Khi đặt điều nhì chén bát lòng trùng nhau, tớ nhận biết rằng những cạnh và những đàng chéo cánh của nhì chén bát lòng này là cùng với nhau, tức là những đàng chéo cánh này còn có nằm trong phỏng nhiều năm và trải qua và một điểm (tâm chén bát diện đều Viết ). Do cơ, Lúc lấy một chén bát lòng và trải rộng lớn nó cho tới một chén bát lòng không giống, tớ rất có thể nhận được một hình vỏ hộp (khối lập phương) với thể tích là 2V1. Vì vậy, thể tích của khối chén bát diện đều được xem vì chưng công thức 2V1.
Hình vuông sở hữu bao nhiêu chén bát diện đều?
Hình vuông sở hữu 6 chén bát diện đều.
Bát diện đều là 1 trong những khối hình học tập được tạo ra trở thành kể từ tư mặt mũi tam giác đều phải có cạnh và diện tích S cân nhau. Trong tình huống của hình vuông vắn, từng cạnh của chính nó tạo ra trở thành một chén bát diện đều.
Để nắm rõ rộng lớn, tớ rất có thể tưởng tượng một hình vuông vắn như 1 hình chữ nhật với phỏng nhiều năm cạnh cân nhau. Hình chữ nhật này còn có tư mặt mũi, nhập cơ nhì mặt mũi đối lập là mặt mũi bên trên và mặt mũi bên dưới, nhì mặt mũi còn sót lại là mặt mũi mặt mũi. Một Lúc những mặt mũi mặt sở hữu cạnh và diện tích S cân nhau, tất cả chúng ta rất có thể gọi bọn chúng là chén bát diện đều.
Vậy, Lúc kiểm tra hình vuông vắn, tớ thấy rằng sở hữu 4 mặt mũi chén bát diện đều - nhì mặt mũi mặt mũi, mặt mũi bên trên và mặt mũi bên dưới. Tuy nhiên, từng mặt mũi bất diện rất có thể được phân thành nhì tam giác đều nên tớ nói theo một cách khác rằng hình vuông vắn cũng có thể có 6 chén bát diện đều.
Mong rằng vấn đề này tiếp tục trả lời được thắc mắc của công ty. Nếu các bạn còn ngẫu nhiên thắc mắc này không giống, hãy nhằm lại cho tới tôi biết!
Tính thể tích khối chén bát diện đều nếu như biết thể tích khối chén bát diện đều cạnh?
Để tính thể tích khối chén bát diện đều, tớ nên biết thể tích khối chén bát diện đều cạnh trước. Thể tích khối chén bát diện đều cạnh (a) được xem theo gót công thức: V = a^3.
Sau cơ, tớ dùng công thức thể tích khối chén bát diện đều: V = 2V1 = 2.a^3. Trong số đó, V1 là thể tích bát diện đều.
Ví dụ, nếu như tớ biết thể tích khối chén bát diện đều cạnh là 5cm, tớ tiếp tục có:
V = 2V1 = 2 x (5cm)^3 = 250cm^3.
Vậy, nếu như biết thể tích khối chén bát diện đều cạnh, tớ rất có thể tính được thể tích khối chén bát diện đều theo gót công thức V = 2V1, với V1 là thể tích bát diện đều cạnh.
Lưu Khối Đa Diện Đều nhập Máy tính Casio và Vinacal Toán 12 Thầy Nguyễn Phan Tiến
Bạn mong muốn tìm hiểu hiểu về khối nhiều diện đều và những đặc điểm lạ mắt của chúng? Hãy coi đoạn phim này nhằm mày mò những kín đáo thú vị về lưu khối nhiều diện đều và tìm hiểu hiểu phương pháp vẽ và đo lường và tính toán chúng!
Giải mến chân thành và ý nghĩa của uỷ thác điểm của đàng chéo cánh nhập chén bát diện đều?
Trong một chén bát diện đều, uỷ thác điểm của đàng chéo cánh là 1 trong những điểm được phân tách song vì chưng đàng chéo cánh. Ý nghĩa của uỷ thác điểm đó là vấn đề cơ nằm tại vị trí trung tâm của chén bát diện đều. Trung tâm này được gọi là O.
Khái niệm \"đường chéo\" nhập chén bát diện đều là đường thẳng liền mạch nối nhì đỉnh ko kề nhau của hình cơ. Trong tình huống chén bát diện đều vuông, đàng chéo cánh là đường thẳng liền mạch trải qua trung điểm của cạnh.
Giao điểm của đàng chéo cánh nhập chén bát diện đều là trung tâm của hình. Như vậy Tức là những đàng kể từ trung tâm cho tới những đỉnh của chén bát diện đều phải có nằm trong phỏng nhiều năm. trái lại, những đàng kể từ trung tâm cho tới những điểm bên trên cạnh của hình cũng có thể có nằm trong phỏng nhiều năm.
Trung tâm của chén bát diện đều là 1 trong những điểm đặc trưng cần thiết nhập hình học tập. Nó rất có thể được dùng nhằm đo lường và tính toán diện tích S, chu vi và thể tích của hình. Trung tâm cũng xác lập những trục đối xứng của hình và thực hiện nổi trội những đặc điểm hình học tập của chính nó.
Xem thêm: asia's economic political and cultural importance is growing
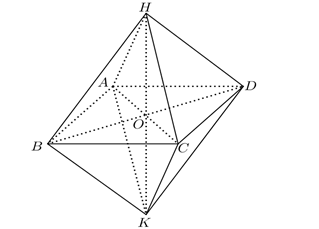
Liệt kê những phần mềm thực tiễn của khối chén bát diện đều nhập cuộc sống đời thường và công nghiệp.
Khối chén bát diện đều, còn được gọi là chén bát diện đều hoặc hình chóp đều, là 1 trong những hình học tập 3 chiều sở hữu 8 mặt mũi, nhập cơ từng mặt mũi là 1 trong những hình vuông vắn và sở hữu nằm trong phỏng nhiều năm cạnh. Dưới đấy là một số trong những phần mềm thực tiễn của khối chén bát diện đều nhập cuộc sống đời thường và công nghiệp:
1. Đồ trang trí: Khối chén bát diện đều thông thường được dùng muốn tạo rời khỏi những vật dụng tô điểm, như tượng nghệ thuật và thẩm mỹ, đèn tô điểm, hoặc những hình dạng lạ mắt không giống. Sự đối xứng và hình dạng thích mắt của khối chén bát diện đều thực hiện cho tới nó trở nên lựa lựa chọn thông dụng muốn tạo rời khỏi những thành phầm tô điểm phát minh.
2. Đóng gói: Khối chén bát diện đều cũng rất có thể được dùng trong những ngành công nghiệp gói gọn nhằm chứa chấp và đảm bảo an toàn những thành phầm. Với hình dạng lập phương và những cạnh đều nhau, khối chén bát diện đều tiện lợi trong các công việc xếp ông xã và bố trí những thành phầm nhằm vận trả hoặc bày sản phẩm.
3. Tạo rời khỏi đối tượng người tiêu dùng 3D: Chúng tớ rất có thể dẫn đến những đối tượng người tiêu dùng 3 chiều bằng phương pháp phối kết hợp những khối chén bát diện đều. Ví dụ, bằng phương pháp xếp ông xã những khối chén bát diện đều lên nhau, tớ rất có thể dẫn đến một tháp nhiều tầng hoặc tòa mái ấm 3 chiều trong những quy mô xây cất hoặc những trò đùa có tiếng như Rubik.
4. Cốc đựng hóa học lỏng: Khối chén bát diện đều cũng rất có thể được dùng thực hiện ly chứa chấp hóa học lỏng, như ly đo, ly đựng nước hoặc ly đựng dung dịch, cũng chính vì hình dạng đều canh ty đáp ứng lượng hóa học lỏng được đo đúng đắn và thuận tiện trong các công việc dùng mỗi ngày.
5. Tính toán hình học: Khối chén bát diện đều cũng có thể có phần mềm nhập đo lường và tính toán hình học tập và lăm le tính những đặc điểm của những hình học tập không giống. Ví dụ, nhập toán học tập, tớ rất có thể dùng phỏng nhiều năm cạnh hoặc thể tích khối chén bát diện đều nhằm đo lường và tính toán những thông số kỹ thuật của những hình học tập không giống, như hình cầu hoặc hình nhập tam giác.
Như vậy, khối chén bát diện đều phải có nhiều phần mềm nhập cuộc sống đời thường và công nghiệp, kể từ tô điểm, gói gọn, tạo ra đối tượng người tiêu dùng 3 chiều, ly đựng hóa học lỏng cho tới đo lường và tính toán hình học tập.
_HOOK_











Bình luận