Một khu vườn hình chữ nhật có chu vi 280m. Người ta làm 1 lối đi xung quanh vườn rộng 2m

Bài luyện giải Việc bằng phương pháp lập hệ phương trình

Bài toán giải bằng phương pháp lập hệ phương trình là tư liệu vì thế đội hình nghề giáo của GiaiToan biên soạn với điều giải cụ thể mang lại dạng bài xích tương quan cho tới những công thức tính diện tích S hình chữ nhật và cơ hội giải Việc bằng phương pháp lập hệ phương trình chung chúng ta học viên nắm rõ những kiến thức và kỹ năng và vận dụng đo lường trong những bài xích luyện. Mời chúng ta học viên nằm trong xem thêm nội dung bài viết.

Đề bài: Một khu vực vườn hình chữ nhật với chu vi 280m. Người tao thực hiện 1 lối chuồn xung xung quanh vườn ( nằm trong khu đất của vườn) rộng lớn 2m. Diện tích sót lại nhằm trồng trọt là 4256m². Tìm diện tích S vườn khi đầu.

Bạn đang xem: một khu vườn hình chữ nhật có chu vi 280m

Hướng dẫn:

Các bước giải Việc bằng phương pháp lập hệ phương trình:

+ Bước 1: Lập hệ phương trình:

* Chọn nhị ẩn và đặt điều ĐK phù hợp mang lại bọn chúng.

* Biểu trình diễn những đại lượng không biết theo đòi những ẩn và những đại lượng đang được biết.

* Lập nhị phương trình biểu thị quan hệ trong số những đại lượng.

+ Bước 2: Giải hệ nhị phương trình phát biểu bên trên.

+ Bước 3: Trả lời: đánh giá coi trong những nghiệm của hệ phương trình, nghiệm này quí phù hợp với Việc và tóm lại .

Lời giải:

Nửa chu vi của khu vực vườn hình chữ nhật là: 280 : 2 = 140m

Gọi chiều lâu năm khu vực vườn hình chữ nhật là a (0 < a < 140, m)

Chiều rộng lớn khu vực vườn hình chữ nhật là b (0 < b < 140, m)

Nửa chu vi của khu vực vườn hình chữ nhật là 140m. Ta với phương trình: a + b = 140 (1)

Người tao thực hiện một lối chuồn xung xung quanh vườn rộng lớn 2m

Xem thêm: trường đại học duy tân học phí

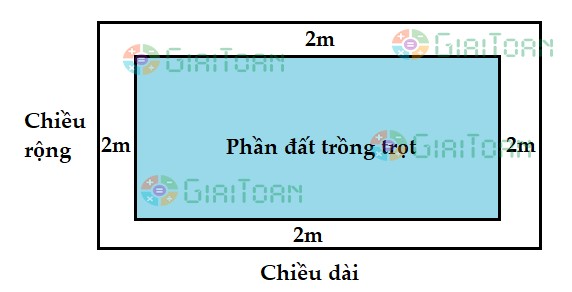
Một khu vực vườn hình chữ nhật với chu vi 280m. Người tao thực hiện 1 lối chuồn xung xung quanh vườn rộng lớn 2m

→ Chiều lâu năm phần khu đất dùng để làm trồng trọt là: a – 4 (m)

Chiều rộng lớn phần khu đất dùng để làm trồng trọt là: b – 4 (m)

Theo đề bài xích, diện tích S khu đất sót lại nhằm trồng trọt là 4256m² nên tao với phương trình:

$\begin{gathered} \left( {a - 4} \right)\left( {b - 4} \right) = 4256 \hfill \\ \Leftrightarrow ab - 4a - 4b + 16 = 4256 \hfill \\ \Leftrightarrow ab - 4\left( {a + b} \right) = 4240\left( 2 \right) \hfill \\ \end{gathered}$

Từ (1) và (2), tao với hệ phương trình:

$\begin{gathered} \left\{ \begin{gathered} a + b = 140 \hfill \\ ab - 4\left( {a + b} \right) = 4240 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} a + b = 140 \hfill \\ ab - 4.140 = 4240 \hfill \\ \end{gathered} \right. \hfill \\ \Leftrightarrow \left\{ \begin{gathered} a + b = 140 \hfill \\ ab = 4800 \hfill \\ \end{gathered} \right. \Leftrightarrow \left\{ \begin{gathered} a = 140 - b\left( 3 \right) \hfill \\ \left( {140 - b} \right)b = 4800\left( 4 \right) \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered}$

Giải phương trình (4) tao được b = 80 (tm) hoặc b = 60 (tm)

Với b = 60 thay cho vô (1) với a = 80 (tm)

Với b = 80 thay cho vô (1) với a = 60 (tm)

Vậy những độ cao thấp của khu vực vườn hình chữ nhật thứu tự là 80m và 60m.

Câu căn vặn liên quan:

Quãng đàng AB lâu năm 100 km. Hai xe hơi lên đường nằm trong 1 khi kể từ A nhằm tiếp cận B
Một xe cộ máy chuồn kể từ A cho tới B với véc tơ vận tốc tức thời và thời hạn dự trù trước
Hai các bạn Hà và Tuấn chuồn xe cộ máy lên đường và một khi kể từ 2 vị trí không giống nhau
Một xe cộ máy chuồn kể từ A cho tới B vô một thời hạn dự tính nếu như véc tơ vận tốc tức thời gia tăng 14km/h thì cho tới sớm rộng lớn 2 giờ
Hai xe hơi chuồn trái hướng kể từ A cho tới B, xuất trị ko nằm trong lúc
Một xe cộ máy chuồn kể từ A cho tới B với véc tơ vận tốc tức thời và thời hạn dự trù trước. Sau khi chuồn được nửa quãng đàng, xe cộ máy gia tăng 10km/h chính vì thế xe cộ máy cho tới B sớm rộng lớn một phần hai tiếng đối với dự tính. Tính véc tơ vận tốc tức thời dự tính của xe cộ máy, biết quãng đàng AB lâu năm 120km.
Tìm nhị số ngẫu nhiên hiểu được tổng của bọn chúng vì chưng 1006 và nếu như lấy số rộng lớn phân tách mang lại số nhỏ thì được thương là 2 và số dư là 124
Một ôtô chuồn kể từ A và dự tính cho tới B khi 12 giờ trưa. Nếu xe đua với véc tơ vận tốc tức thời 35km/h thì sẽ tới B chậm trễ 2 tiếng đồng hồ đối với quy ấn định. Nếu xe đua với véc tơ vận tốc tức thời 50km/h thì sẽ tới B sớm 1 giờ đối với dự tính. Tính phỏng lâu năm quãng đàng AB và thời gian xuất trị của xế hộp bên trên A.
Giải Việc cổ sau Quýt, cam mươi bảy ngược tươi tỉnh Đem phân tách cho 1 trăm con người nằm trong vui
Giải Việc bằng phương pháp lập hệ phương trình dạng gửi động
Một khu vực vườn hình chữ nhật với chu vi 280m. Người tao thực hiện 1 lối chuồn xung xung quanh vườn ( nằm trong khu đất của vườn) rộng lớn 2m. Diện tích sót lại nhằm trồng trọt là 4256m². Tìm diện tích S vườn khi đầu.
Hai xe hơi chuồn trái hướng kể từ A cho tới B, xuất trị ko nằm trong lúc
Cho tam giác ABC vuông bên trên A. bên trên AC lấy một điểm M và vẽ đàng tròn trĩnh 2 lần bán kính MC. Kẻ BM hạn chế đàng tròn trĩnh bên trên D. Đường trực tiếp DA hạn chế đàng tròn trĩnh bên trên S. Chứng minh rằng:a. ABCD là 1 trong những tứ giác nội tiếpb. $\widehat {ABD} = \widehat {ACD}$ c. CA là tia phân giác của góc SCB.
Cho nửa đàng tròn trĩnh tâm O 2 lần bán kính AB, C là 1 trong những điểm nằm trong lòng O và A. Đường trực tiếp vuông góc với AB bên trên C hạn chế nửa đàng tròn trĩnh bên trên trên I, K là 1 trong những điểm ở bất kì bên trên đoạn trực tiếp CI (K không giống C và I) tia AK hạn chế nửa đàng tròn trĩnh O bên trên M tia BM hạn chế tia CI bên trên D.Chứng minh:a) Các tứ giác ACMD, BCKM nội tiếp đàng trònb) CK.CD = CA.CBc) Gọi N là phú điểm của AD và đàng tròn trĩnh O minh chứng B, K, N trực tiếp hàngd) Tâm đàng tròn trĩnh nước ngoài tiếp tam giác AKD phía trên một đường thẳng liền mạch thắt chặt và cố định khi K địa hình bên trên đoạn trực tiếp CI

Tham khảo tăng những dạng bài xích giải Việc lớp 8, lớp 9:

Xem thêm: các từ chỉ sự vật

Giải Việc bằng phương pháp lập hệ phương trình
Giải Việc bằng phương pháp lập hệ phương trình dạng năng suất
Giải Việc bằng phương pháp lập hệ phương trình dạng dò la số
Giải Việc bằng phương pháp lập hệ phương trình dạng thực hiện cộng đồng thực hiện riêng
Giải Việc bằng phương pháp lập phương trình lớp 8 Toán gửi động

---------

Như vậy, GiaiToan.com đang được gửi cho tới chúng ta học viên Giải Việc bằng phương pháp lập hệ phương trình. Dường như, chúng ta học viên rất có thể xem thêm tăng những tư liệu và những công thức không giống khác vì thế GiaiToan biên soạn nhằm học tập chất lượng tốt môn Toán rộng lớn. Với phiếu bài xích luyện này sẽ hỗ trợ chúng ta tập luyện tăng khả năng giải đề và thực hiện bài xích chất lượng tốt rộng lớn. Chúc chúng ta tiếp thu kiến thức tốt!

Chia sẻ bởi: Ỉn