Mặt ước, khối ước là những khái niệm cực kỳ quen thuộc thuộc nhập hình học trung học. Tuy nhiên, ko phải ai cũng nhớ chính xác được công thực tính không gian mặt ước, thể thích khối ước. Thông qua chuyện bài viết trên đây, Hoàng Hà Mobile sẽ cung cấp công thức thể tích hình ước để khách hàng có thể tham lam khảo và áp dụng nhập các bài toán hình học.
Định nghĩa mặt ước là gì? Khối ước là gì? Hình ước là gì?
Trước Khi tìm hiểu ngầm công thức tính thể tích hình ước là gì thì khách hàng phải nắm rõ được các khái niệm và định nghĩa về mặt ước, khối ước và hình ước. Trong không khí hình học phụ vương chiều, Khi một nửa hình tròn có tâm O, bán kính R xoay một vòng xung đường kính có độ dài AB được cố định thì đi ra được một hình ước. Trong đó bao gồm:
Bạn đang xem: công thức tính thể tích hình cầu
- Phẩn nửa đường tròn Khi xoay là phần một mặt ước.
- Tâm O chính là tâm của hình ước với bán kính là R của mặt ước hoặc hình ước đó.

Khái niệm mặt ước là không khí tập những điểm cách đều tâm O hình câu với một khoảnh cách bán kính R ko đổi. Trong trường hợp này nghĩa là R = OA. Hình ước có tính chất là hình có một trục đối xứng là đường thẳng bất kỳ có thể phó nhau Khi trải qua tâm của hình ước. Lúc này, khách hàng chỉ nên xoay quả ước xung xung quanh phần trục này ở bất kỳ góc độ nào cũng thấy được chính quả ước này là chính nó.
Bên cạnh đó, phần mặt phẳng phản xạ được định nghĩa là mặt phẳng được cắt hình về được đề cập trải qua tâm của hình và phân chia quả ước thành nhị nửa bằng nhau.
Công thức xác định không gian mặt ước và thể tích hình ước là gì?
Dưới trên đây là công thức tính không gian của mặt ước và thể tích của hình cầu mà khách hàng nên biết:
Công thức xác định không gian của mặt cầu
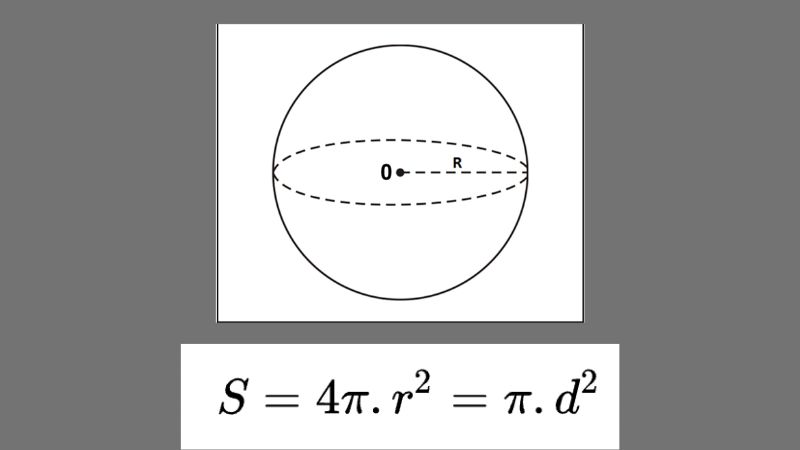
Theo định nghĩa nhập hình học, không gian của mặt ước sẽ được xác định bằng 4 lần không gian của hình tròn lớn hoặc tích 4 lần của hằng số Pi cùng với bán kính R được bình phương của khối ước. Công thức tổng quát đó là: S= 4π. r^2=π.d2. Các yếu tố nhập đó bao gồm:
- S được định nghĩa là không gian của mặt ước.
- r được định nghĩa là bán kính của mặt ước hoặc của hình ước.
- d được định nghĩa là đường kính của mặt ước hoặc của hình ước.
- π được định nghĩa là hằng số, có giá trị xấp xỉ 3.14.
Công thức xác định không gian xung xung quanh của hình cầu
Để có thể xác định được không gian xung xung quanh của hình ước, khách hàng có thể áp dụng công thức: Sxq= 4πr^2. Các yếu tố nhập công thức bao gồm:
- Sxq được định nghĩa là phần không gian xung xung quanh của hình ước.
- π được định nghĩa là hằng số, có giá trị xấp xỉ 3.14.
- r được định nghĩa là bán kính của hình ước.
Khi sử dụng công thức, này khách hàng chỉ nên nhân bán kính R hình ước với 2, rồi được kết quả nhân với số π để có thể tính được không gian S xung xung quanh của hình ước.
Công thức xác định thể tích hình cầu
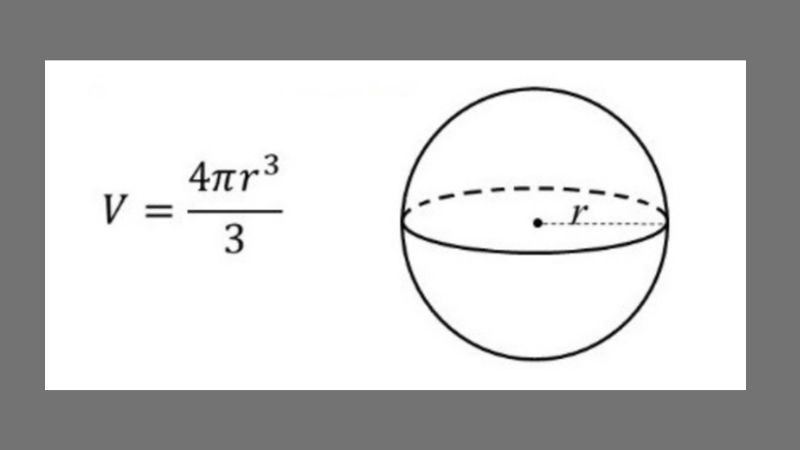
Về khái niệm hình học, thể tích của hình cầu hoặc còn gọi là khối ước được xác định bằng bốn phần phụ vương của số Pi nhân với bán kính lập phương của hình ước. Do đó, để có thể tính được thể tích của khối ước thì khách hàng chỉ nên phải tìm được bán kính của hình ước hoặc đường kính hình ước rồi áp dụng vào công thức V= 4/3 x π x r^3. Các yếu tố nhập công thức bao gồm:
- V được định nghĩa là thể tích của hình ước có đơn vị m3.
- π được định nghĩa là hằng số, có giá trị xấp xỉ 3.14.
- r được định nghĩa là bán kính của hình ước.
- d được định nghĩa là bán kính của mặt ước hoặc hình ước.
Hướng dẫn chi tiết thao tác tính thể tích hình cầu
Để tính được thể tích thì khách hàng cần thực hiện thao tác cụ thể dưới đây:
Bước 1: Đầu tiên, viết ra sức thức xác định thể tích của hình ước đi ra giấy đó là: V = ⁴⁄₃π.r³.
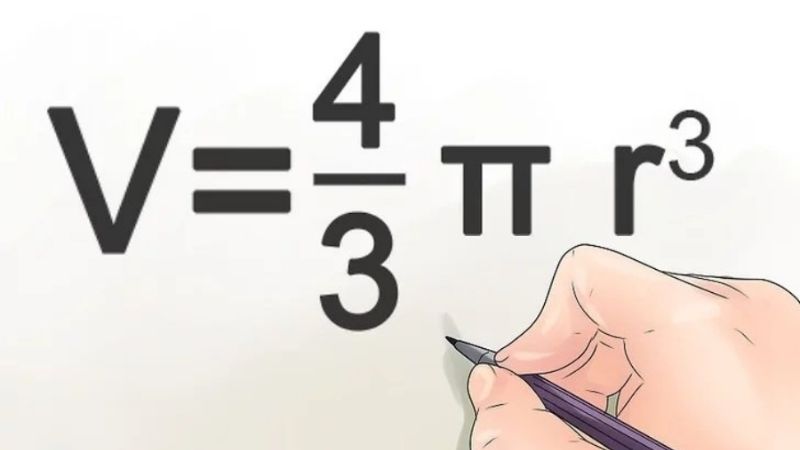
Bước 2: Sau đó, khách hàng cần phát âm thật kỹ đề bài để tìm bán kính của hình ước. Nếu đề đã cung cấp vấn đề bán kính sẵn thì chỉ nên ghi đi ra giấy. Tuy nhiên, nếu đề cho tới vấn đề về đường kính của hình tròn thì khách hàng có thể sử dụng công thức thể tích V = 1⁄6π.d³ để tính. Bạn cũng có thể sử dụng phương pháp đường kính phân chia song để đi ra được kết quả bán kính rồi tiến hành áp dụng công thức ở bước 1.
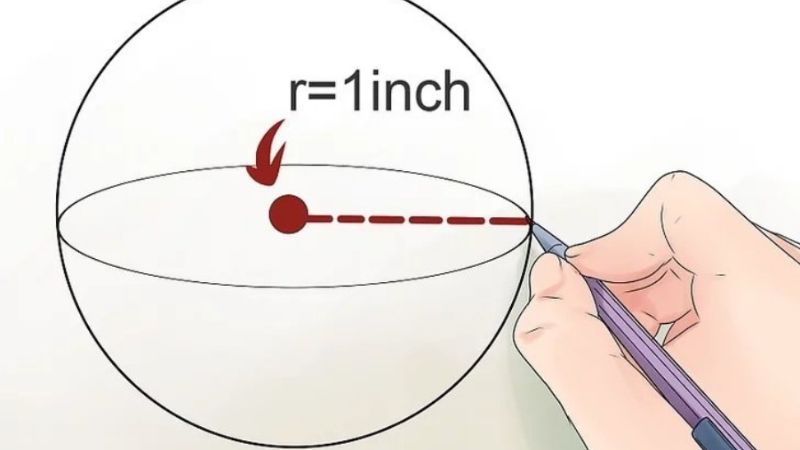
Trong trường hợp khó rộng lớn Khi đề bài chỉ cho tới khách hàng vấn đề về không gian của mặt ước S thì khách hàng hoàn toàn có thể tìm bán kính hình tròn bằng cách tiến hành lấy không gian của mặt ước phân chia cho tới 4pi. Sau đó, khách hàng sẽ tính căn bậc nhị của kết quả vừa tính là đi ra được.
Bước 3: Tiếp bám theo, khách hàng chỉ nên tiến hành tính lũy thừa của bán kính r bằng việc sử dụng bán kính của hình tròn nhân phụ vương lần chính nó hoặc thổi lên số mũ bằng phụ vương.
Xem thêm: thúy kiều mang họ gì
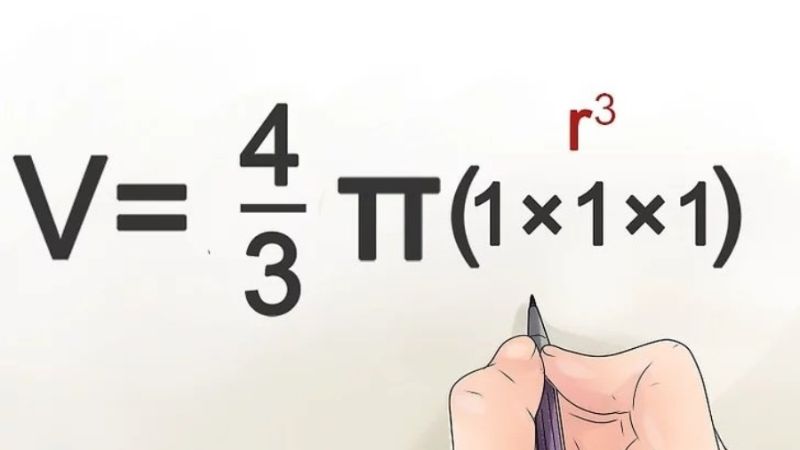
Bước 4: Bạn sẽ thay cho thế giá trị của bán kính lũy thừa căn bậc phụ vương vào công thức thể tích hình ước để phương trình trở nên gọn rộng lớn.
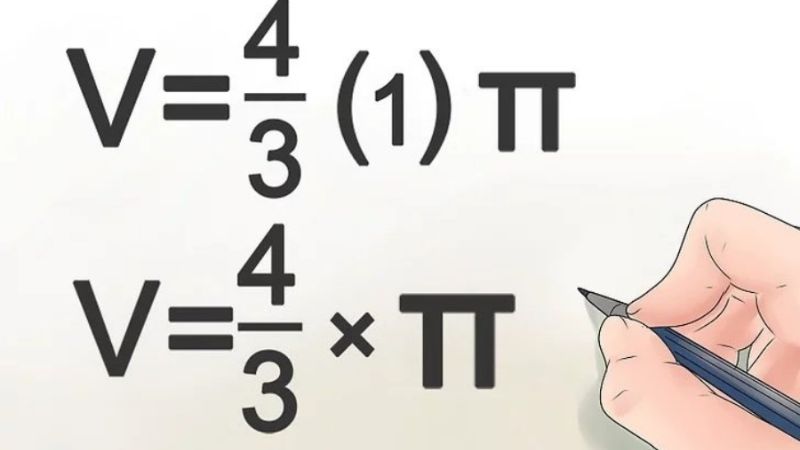
Bước 5: Tiến hành để hằng số pi vào nhập phép tinh nghịch và nhân giá trị xấp xỉ 3.14 với 4/3 hoặc để nguyên vẹn ký hiệu π nhập bài bám theo dạng đó là V= 4/3π là đã hoàn thành.
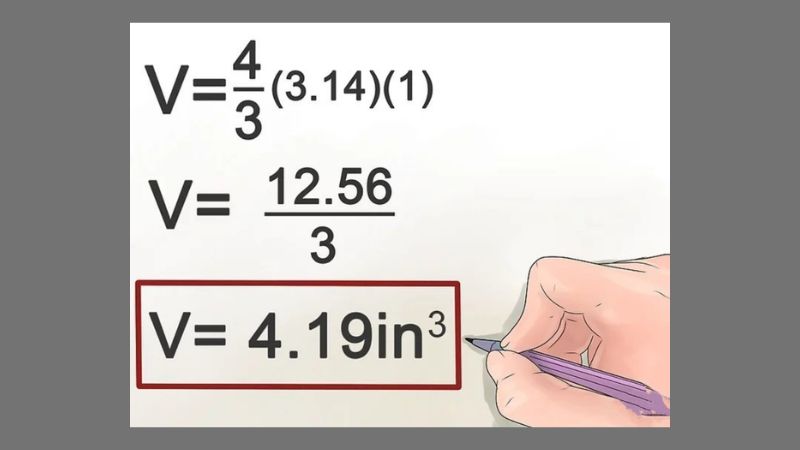
Vì sao không gian của mặt ước bằng 4 lần không gian của hình tròn lớn?
Ngoài công thức tính thể tích hình ước, một số người còn thắc mắc vì sao không gian của mặt ước được tính bằng 4 không gian của hình tròn lớn. Theo lý thuyết, không gian của mặt ước là tổng của không gian những hình tròn được tạo thành bề mặt của hình ước. Do đó, nếu khách hàng nắm được công thức xác định không gian của hình tròn thì khách hàng sẽ tính toán được phần không gian của mặt ước.
Công thức xác định không gian của hình tròn đó là S= π. r^2, trong đó S được gọi là không gian hình tròn, r được gọi là bán kính hình tròn. Khi xác định không gian của mặt ước, tao sẽ tính toàn bộ tổng của không gian các hình trọn được tạo thành từ bề mặt của hình ước. Mỗi hình tròn có bên trên bề mặt hình ước sẽ có cùng bán kính nên có thể gọi bán kính của hình tròn ký hiệu R. Phần không gian của hình tròn bên trên một bề mặt hình ước được ký hiệu là S1= π. r^2.
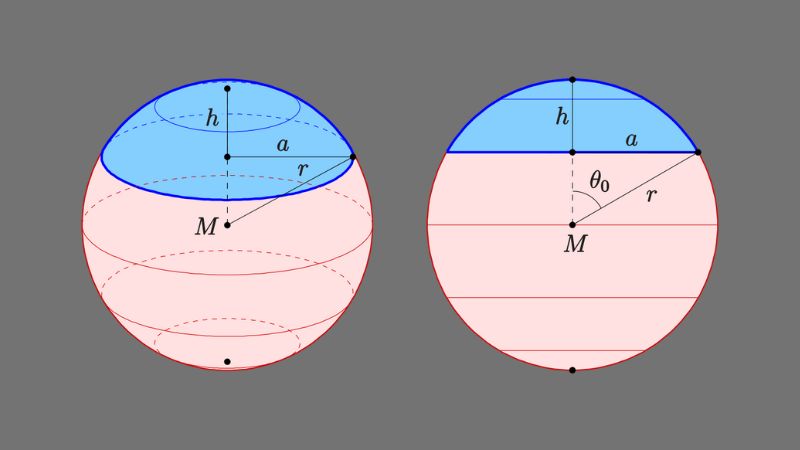
Diện tích của phần mặt ước có cấu tạo từ 4 hình tròn sẽ tạo đi ra một mặt phẳng. Bởi tất cả các hình tròn này đều có cùng một bán kính nên tổng không gian của 4 hình tròn này sẽ bằng S1+S2+S3+S4= 4πR^2.
Chính vì vậy, có thể nói rằng không gian của mặt ước sẽ bằng 4 lần của không gian của hình tròn lớn được xác định với công thức S = 4πR^2. Với công thức này đã có thể chứng minh được rõ ràng nhập việc áp dụng định lý tính không gian của mặt ước.
Vì sao không gian của mặt ước bằng 4 lần hằng số π nhân bình phương bán kính R?
Ngoài công thức thể tích hình ước được nêu bên trên thì một số người thắc mắc thao tác tính không gian của mặt ước với công thức: S= 4π. r^2.
- Đầu tiên, cần xác định được bán kính của hình ước trải qua đường kính của hình ước hoặc bán kính được đo trực tiếp.
- Tiếp bám theo bán kính R bình mùi hương bằng cách nhân đường kính. Lưu ý, phần không gian của mặt ước là tổng tất cả không gian các hình tròn lớn với cùng độ dài bán kính R.
- Sử dụng công thức xác định không gian của mặt ước đó là S= 4π. r^2.
- Cuối cùng sử dụng công thức bên trên tích nhân với số 4 và hằng số Pi cùng bình phương độ dài bán kính R để có thể tính được không gian của mặt ước.

Mối quan tiền hệ giữa bán kính R và thể tích hình cầu
Thể tích hình cầu là lượng vật hóa học tuy nhiên khối cầu cướp lưu giữ. Nó tùy theo nửa đường kính của khối cầu. Bán kính là khoảng cách kể từ tâm khối cầu cho tới một điểm ngẫu nhiên bên trên mặt phẳng của khối cầu. Công thức tính thể tích khối cầu là: V= 4/3 x π x r^3, có các yếu tố bao gồm:
- V được định nghĩa là thể tích của khối cầu
- r được định nghĩa là nửa đường kính của khối cầu
- π được định nghĩa là hằng số Pi với độ quý hiếm xấp xỉ là 3.14
Như vậy, nếu như nửa đường kính của khối cầu tăng gấp hai thì thể tích khối cầu tiếp tục tăng vội vàng tám chuyến. Ví dụ, nếu như nửa đường kính của khối cầu là một trong những centimet thì thể tích của khối cầu này đó là 4/3π cm³. Nếu nửa đường kính của khối cầu tạo thêm 2 centimet thì thể tích của khối cầu tiếp tục tạo thêm trở thành 64/3π cm³.
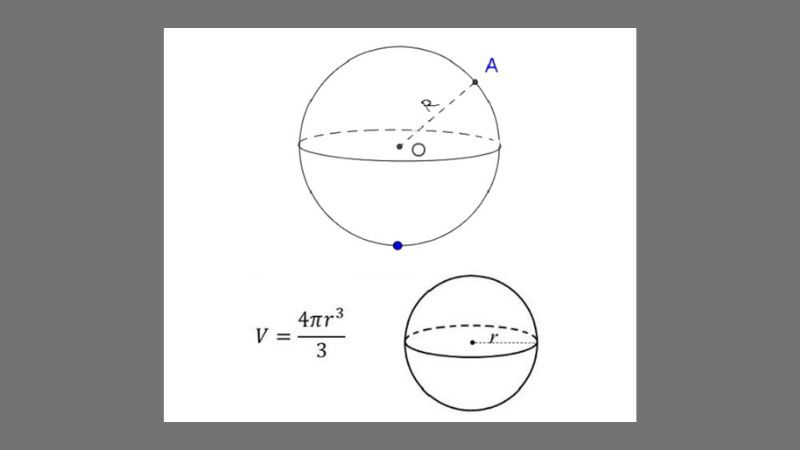
Có thể lý giải quan hệ này như sau: Khối cầu là 1 trong hình thể phụ vương chiều, đem nửa đường kính là 2 lần bán kính của chính nó. Bán kính càng rộng lớn thì khối cầu càng rộng lớn, thể tích của khối cầu cũng càng rộng lớn. Do bại, thể tích của hình cầu tỉ trọng với một khối của nửa đường kính lập phương.
Công thức xác lập thể tích của hình cầu đem phần mềm rộng thoải mái trong tương đối nhiều nghành nghề dịch vụ, bao gồm:
Xem thêm: hầm hải vân dài bao nhiêu km
- Về lĩnh vực toán học: Công thức này được dùng trong những việc về hình học tập không khí, ví dụ như tính thể tích của những vật thể đem hình cầu, như trái khoáy bóng, trái khoáy khu đất,…
- Kiến trúc: Công thức này được dùng nhập kiến thiết và thi công những công trình xây dựng đem hình cầu, ví dụ như hồ nước nước, bể chứa chấp, vòi vĩnh phun nước,…
- Công nghệ xây dựng: Công thức này được dùng nhập đo lường lượng vật tư quan trọng nhằm thi công những công trình xây dựng đem hình cầu như cầu, tầng hầm,…
- Vật lý: Công thức này được dùng nhập đo lường lượng của những vật thể đem hình cầu như chất khí, chất lỏng,…
- Cơ học: Thể tích của hình ước được dùng nhập đo lường lực tính năng lên những vật thể hình ước có các tác động cơ học như quả bóng nảy lên khỏi mặt đất,..

Tổng kết
Thông qua chuyện nội dung bài viết bên trên chúng ta tiếp tục hiểu rằng công thức xác lập diện tích S mặt mày cầu và thể tích hình cầu được thiết lập ra làm sao. Ngoài ra, chúng ta cũng hiểu rằng cơ hội xác lập thể tích cuark ăn năn cầu từng bước cụ thể và quan hệ của chính nó với những nguyên tố không giống đem nhập hình cầu. Hy vọng Hoàng Hà Mobile tiếp tục cung ứng những kỹ năng và kiến thức cần thiết và hữu ích về toán học tập nhằm độc giả hoàn toàn có thể làm rõ và bám theo dõi.
Xem thêm:
- Khối D07 bao gồm môn đua này, ngành đua nào?
- Công thức tính thể tích hình cầu và diện tích S hình cầu










Bình luận