Bách khoa toàn thư ngỏ Wikipedia
| Hình học | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
 Hình chiếu một phía cầu lên trên bề mặt phẳng phiu. Bạn đang xem: chân đường vuông góc là gì | ||||||||||
| ||||||||||
|
Phân nhánh
|
||||||||||
|
Khái niệm Chiều
|
||||||||||
|
Không chiều
|
||||||||||
|
Một chiều
|
||||||||||
|
Hai chiều
|
||||||||||
|
Ba chiều
|
||||||||||
|
Bốn chiều / số chiều khác
|
||||||||||
| Nhà hình học | ||||||||||
|
theo tên
|
||||||||||
|
theo giai đoạn
|
||||||||||
|
Trong hình học tập sơ cấp cho, đặc điểm vuông góc là quan hệ thân thích hai tuyến đường trực tiếp nhưng mà tạo nên trở thành một góc vuông (90 độ). Tính hóa học này cũng rất được không ngừng mở rộng cho những đối tượng người dùng hình học tập không giống.
Một đường thẳng liền mạch được rằng là vuông góc một đường thẳng liền mạch không giống nếu như và chỉ nếu như hai tuyến đường trực tiếp rời nhau ở góc cạnh vuông.[1] Cụ thể rộng lớn, nếu như lối thằng loại nhất vuông góc với đường thẳng liền mạch loại nhì nếu như (1) hai tuyến đường trực tiếp rời nhau; và (2) và bên trên phó điểm góc bẹt bên trên một phía của đường thẳng liền mạch loại nhất bị rời vày đường thẳng liền mạch loại nhì trở thành nhì góc tương đẳng. Tính vuông góc thể hiện nay tính đối xứng, tức là nếu như đường thẳng liền mạch loại nhất vuông góc với đường thẳng liền mạch loại nhì, thì đường thẳng liền mạch loại nhì cũng vuông góc với đường thẳng liền mạch loại nhất. Vì nguyên do này, tớ nói theo một cách khác hai tuyến đường trực tiếp vuông góc cùng nhau nhưng mà ko cần thiết xác lập trật tự ưu tiên.
Tính hóa học vuông góc hoàn toàn có thể đơn giản dễ dàng không ngừng mở rộng rời khỏi mang đến so với những đoạn trực tiếp và tia. Ví dụ, một quãng trực tiếp vuông góc với đoạn trực tiếp nếu như, khi từng đoạn trực tiếp được không ngừng mở rộng kéo dãn dài về nhì phía sẽ tạo trở thành một đường thẳng liền mạch, hai tuyến đường trực tiếp sản phẩm này tự động hóa tuân theo dõi khái niệm vuông góc phía trên. bằng phẳng ký hiệu, tức là đoạn trực tiếp AB vuông góc với đoạn trực tiếp CD.[1]
Một đường thẳng liền mạch vuông góc với một phía phẳng phiu nếu như và chỉ nế như đó vuông góc với từng đường thẳng liền mạch ở trong mặt mày phẳng phiu bại và rời với đường thẳng liền mạch này. Định nghĩa này tùy thuộc vào khái niệm hai tuyến đường trực tiếp vuông góc cùng nhau.
Hai mặt mày phẳng phiu vô không khí vuông góc cùng nhau nếu như góc nhị diện thân thích bọn chúng thực hiện trở thành một góc vuông (90 độ).
Tính hóa học vuông góc là 1 trong những tình huống đặc trưng của định nghĩa toán học tập tổng quát tháo rộng lớn là tính trực giao; vuông góc là tính trực phó của lớp những đối tượng người dùng hình học tập hạ tầng. Do vậy, vô toán học tập thời thượng, kể từ "vuông góc" song khi được dùng nhằm mục đích mô tả những ĐK trực phó hình học tập phức tạp rộng lớn, như trong số những mặt mày phẳng phiu và những vectơ trực chuẩn chỉnh (normal) của bọn chúng.
Quan hệ vuông góc vô mặt mày phẳng[sửa | sửa mã nguồn]
Hai đường thẳng liền mạch vuông góc[sửa | sửa mã nguồn]
Có một và có một đường thẳng liền mạch trải qua một điểm và vuông góc với đường thẳng liền mạch mang đến trước
Dựng hai tuyến đường vuông góc[sửa | sửa mã nguồn]

Dựng lối vuông góc (lam) với đường thẳng liền mạch AB trải qua điểm Phường.
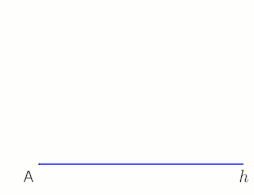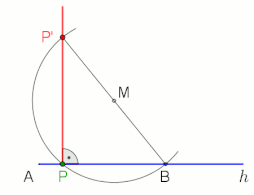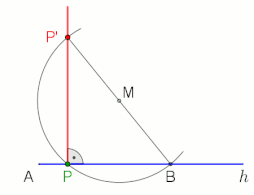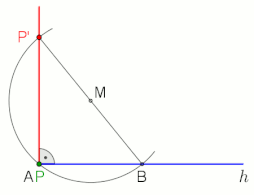
Hình động minh họa cơ hội dựng lối vuông góc với đường thẳng liền mạch g bên trên điểm Phường (áp dụng không chỉ là ở điểm mút A, M chọn 1 cơ hội tự động do).
Xem thêm: trường đại học duy tân học phí
Để dựng một đường thẳng liền mạch vuông góc với đường thẳng liền mạch AB qua chuyện điểm Phường dùng thước kẻ và compa, tiến hành công việc như sau (xem hình mặt mày trái):
- Bước 1 (đỏ): dựng một lối tròn xoe với tâm bên trên Phường sở hữu tâm ngẫu nhiên sao mang đến lối tròn xoe rời đường thẳng liền mạch AB bên trên nhì điểm A' và B', nhưng mà cơ hội đều kể từ Phường.
- Bước 2 (lục): dựng hai tuyến đường tròn xoe sở hữu tâm theo thứ tự bên trên A' và B' và sở hữu nửa đường kính cân nhau. Gọi Q và R ứng là những phó điểm của hai tuyến đường tròn xoe này.
- Bước 3 (lam): nối Q và R nhằm nhận được đường thẳng liền mạch PQ ước muốn.
Để chứng tỏ PQ vuông góc với AB, dùng lăm le lý tam giác đồng dạng CCC mang đến nhì tam giác QPA' và QPB' nhằm tiếp cận Kết luận nhì góc OPA' và OPB' cân nhau. Sau bại dùng lăm le lý tam giác đồng dạng CGC mang đến nhì tam giác OPA' và OPB' nhận được nhì góc POA và POB cân nhau.
Để vẽ một đường thẳng liền mạch vuông góc với đường thẳng liền mạch bên trên hoặc trải qua điểm Phường dùng lăm le lý Thales, coi hình động cạnh bên.
Cũng hoàn toàn có thể vận dụng lăm le lý Pytago nhằm thực hiện hạ tầng mang đến cách thức dựng góc vuông. Ví dụ, bằng phương pháp dùng tía đoạn thước sở hữu tỉ lệ thành phần phỏng nhiều năm 3:4:5 sẽ tạo rời khỏi hình một tam giác vuông. Phương pháp này cực kỳ thuận tiện mang đến bịa sắp xếp những dụng cụ và địa điểm bên trên mảnh đất nền hoặc quần thể vườn rộng lớn, và khi phỏng đúng chuẩn ko đòi hỏi cao. Tam giác vuông này hoàn toàn có thể tái diễn bất kể khi nào là quan trọng.
Chân lối vuông góc - hình chiếu vuông góc của một điểm lên lối thẳng[sửa | sửa mã nguồn]

Từ chân thông thường được dùng thông thường xuyên kèm theo với định nghĩa vuông góc. Cách dùng này được minh họa vô hình vẽ phía trên, và phần chú thích của hình. Hình vẽ được bố trí theo hướng ngẫu nhiên. Và chân lối vuông góc ko nhất thiết nên nằm ở vị trí lòng. Chân lối vuông góc còn được gọi là hình chiếu vuông góc của điểm lên đường thẳng liền mạch.

Đường vuông góc, lối xiên và hình chiếu của lối xiên[sửa | sửa mã nguồn]
Trong toàn bộ những đoạn trực tiếp kẻ từ một điểm ở ngoài một đường thẳng liền mạch và rời đường thẳng liền mạch bại, đoạn vuông góc là đoạn trực tiếp sớm nhất và có một không hai. Các đoạn trực tiếp còn sót lại được gọi là lối xiên.
Đoạn trực tiếp số lượng giới hạn vày chân lối vuông góc và phó điểm của lối xiên với đường thẳng liền mạch được gọi là hình chiếu của lối xiên lên đường thẳng liền mạch bại.
Trong những lối xiên kẻ từ là một điểm ở ngoài đường thẳng liền mạch cho tới đường thẳng liền mạch đó:
- Đường xiên to hơn (hoặc nhỏ hơn) thì sở hữu hình chiếu to hơn (hoặc nhỏ hơn) và ngược lại
- 2 lối xiên cân nhau thì sở hữu hình chiếu cân nhau và ngược lại
Quan hệ vuông góc vô ko gian[sửa | sửa mã nguồn]
Đường trực tiếp vuông góc với mặt mày phẳng[sửa | sửa mã nguồn]
Đường trực tiếp vuông góc với mặt mày phẳng phiu khi đường thẳng liền mạch bại vuông góc với từng đường thẳng liền mạch vô mặt mày phẳng phiu đó
Nếu đường thẳng liền mạch vuông góc với 2 đường thẳng liền mạch rời nhau vô và một mặt mày phẳng phiu thì đường thẳng liền mạch bại vuông góc với mặt mày phẳng phiu chứa chấp 2 đường thẳng liền mạch bại.
Có 1 và chỉ 1 đường thẳng liền mạch cút sang 1 điểm ở bề ngoài phẳng phiu và vuông góc với mặt mày phẳng phiu bại.
Có 1 và chỉ một mặt phẳng phiu cút sang 1 điểm ở ngoài đường thẳng liền mạch và vuông góc với đường thẳng liền mạch bại.
Phép chiếu vuông góc[sửa | sửa mã nguồn]
Cho đường thẳng liền mạch (d) vuông góc với mặt mày phẳng phiu (P). Phép chiếu tuy vậy song theo dõi phương của (d) được gọi là luật lệ chiếu vuông góc lên trên bề mặt phẳng phiu (P).
Kết trái ngược của luật lệ chiếu vuông góc được gọi hình chiếu vuông góc.
Quy ước: nếu như rằng luật lệ chiếu (hoặc hình chiếu) nhưng mà ko rằng gì thêm thắt, tớ coi như này là luật lệ chiếu (hoặc hình chiếu) vuông góc.
Đường trực tiếp vuông góc vô ko gian[sửa | sửa mã nguồn]
Trong không khí, 2 đường thẳng liền mạch vuông góc cùng nhau hoàn toàn có thể rời nhau hoặc chéo cánh nhau
Cho đường thẳng liền mạch (a) ko vuông góc với mặt mày phẳng phiu (P) và đường thẳng liền mạch , khi đó với (b') là hình chiếu của (a) lên (P)
2 mặt mày phẳng phiu vuông góc[sửa | sửa mã nguồn]
Điều khiếu nại nhằm 2 mặt mày phẳng phiu vuông góc[sửa | sửa mã nguồn]
Điều khiếu nại cần thiết và đầy đủ nhằm 2 mặt mày phẳng phiu vuông góc là mặt mày phẳng phiu này có một đường thẳng liền mạch vuông góc với mặt mày phẳng phiu bại.
Tính chất[sửa | sửa mã nguồn]
2 mặt mày phẳng phiu vuông góc cùng nhau thì bất kể đường thẳng liền mạch nào là nằm ở vị trí một trong những 2 mặt mày phẳng phiu vuông góc với phó tuyến của 2 mặt mày phẳng phiu bại thì đường thẳng liền mạch bại vuông góc với mặt mày phẳng phiu bại.
Xem thêm: điểm chuẩn học viện báo chí và tuyên truyền 2022
2 mặt mày phẳng phiu (P) và (Q) vuông góc cùng nhau thì đường thẳng liền mạch trải qua một điểm vô mặt mày phẳng phiu (P) vuông góc với mặt mày phẳng phiu (Q) thì tiếp tục luôn luôn ở trong (P)
2 mặt mày phẳng phiu rời nhau nằm trong vuông góc với mặt mày phẳng phiu loại 3 thì phó tuyến của 2 mặt mày phẳng phiu này sẽ vuông góc với mặt mày phẳng phiu loại 3.
Có có một không hai một phía phẳng phiu trải qua một đường thẳng liền mạch và vuông góc với một phía phẳng phiu ko vuông góc với đường thẳng liền mạch bại.
Xem thêm[sửa | sửa mã nguồn]
- Thành phần pháp tuyến và tiếp tuyến
- Pháp tuyến
Tham khảo[sửa | sửa mã nguồn]
- ^ a b Kay (1969, tr. 91)
- ^ Kay (1969, tr. 114)
Thư mục[sửa | sửa mã nguồn]
- Altshiller-Court, Nathan (1925), College Geometry: An Introduction to tướng the Modern Geometry of the Triangle and the Circle (ấn phiên bản 2), New York: Barnes & Noble, LCCN 52-13504
- Kay, David C. (1969), College Geometry, New York: Holt, Rinehart and Winston, LCCN 69-12075
- Phan Đức Chính và người cùng cơ quan, Sách giáo khoa Toán 7 - tập dượt 1, Nhà xuất phiên bản dạy dỗ Việt Nam
- Phan Đức Chính và người cùng cơ quan, Sách giáo khoa Toán 7 - tập dượt 2, Nhà xuất phiên bản dạy dỗ Việt Nam
- Trần Văn Hạo và người cùng cơ quan, Sách giáo khoa Hình học tập 11, Nhà xuất phiên bản dạy dỗ Việt Nam
- Đoàn Quỳnh và người cùng cơ quan, Sách giáo khoa Hình học tập 11 Nâng cao, Nhà xuất phiên bản dạy dỗ Việt Nam
Liên kết ngoài[sửa | sửa mã nguồn]
- Definition: perpendicular with interactive animation.
- How to tướng draw a perpendicular bisector of a line with compass and straight edge (animated demonstration).
- How to tướng draw a perpendicular at the endpoint of a ray with compass and straight edge (animated demonstration).
















Bình luận